Résonance paramétrique en électronique
- Étudier les caractéristiques de la résonance paramétrique pour les excitations sinusoïdales et carré,
- déterminer les bandes de résonance.
Montage expérimental dans le cas où le signal pompe est continu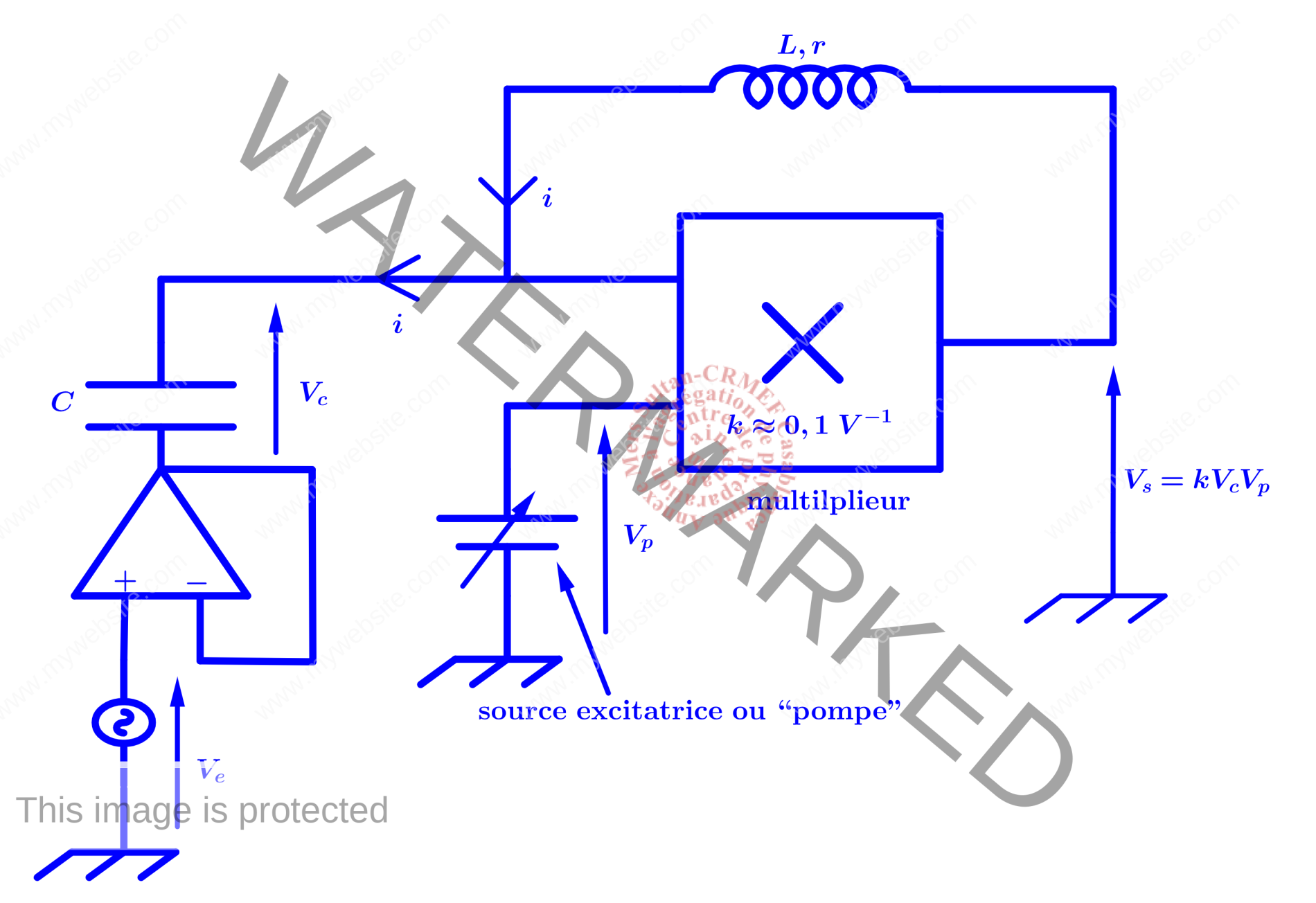
Montage expérimental dans le cas où le signal pompe est sinusoïdal et carré
- Carte d’acquisition+PC,
- oscilloscope numérique,
- GBF,
- multiplieur AD633JN, ampli. Op. TL081,
- bobine d’inductance 36 mH,
- boite à décades de capacités,
- fils électriques
1. Définition de la résonance paramétrique :
C’est la naissance et le maintient des oscillations d’un oscillateur(RLC) lorsqu’on agit périodiquement sur l’un des paramètres déterminant la fréquence propre de cet oscillateur. L’oscillateur entre en résonance lorsque la fréquence du signal pompe appartient à un intervalle centré sur le double de la fréquence propre de l’oscillateur. la résonance paramétrique correspond à une instabilité du système.2. Cas où le signal pompe est continu
Considérons le montage de la figure ci-dessous.  L’équation différentielle vérifiée par la tension $V_c$ s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}V_s=kV_pV_c ;\ ;V_s-V_c=ri+L\frac{di}{dt} ;\ ;i=C\frac{dV_c}{dt}\Downarrow\\ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2\left(1-kV_p\right)V_c=0 ;\ ;\omega_0=\frac{1}{\sqrt{LC}} ;\ ;Q=\frac{1}{r}\sqrt{\frac{L}{C}}\\ V_p=0\Rightarrow \underbrace{ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2V_c=0}_{\text{oscillateur harmonique amorti}}\\ V_p=cste\Rightarrow \underbrace{\frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\frac{1}{\frac{LC}{(1-kV_p)}}V_c=0}_{\text{Oscillateur RLC dont la frequence propre est modifiee par la constante }V_p}\end{gathered}\right.
L’équation différentielle vérifiée par la tension $V_c$ s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}V_s=kV_pV_c ;\ ;V_s-V_c=ri+L\frac{di}{dt} ;\ ;i=C\frac{dV_c}{dt}\Downarrow\\ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2\left(1-kV_p\right)V_c=0 ;\ ;\omega_0=\frac{1}{\sqrt{LC}} ;\ ;Q=\frac{1}{r}\sqrt{\frac{L}{C}}\\ V_p=0\Rightarrow \underbrace{ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2V_c=0}_{\text{oscillateur harmonique amorti}}\\ V_p=cste\Rightarrow \underbrace{\frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\frac{1}{\frac{LC}{(1-kV_p)}}V_c=0}_{\text{Oscillateur RLC dont la frequence propre est modifiee par la constante }V_p}\end{gathered}\right.
\end{eqnarray*} Cas où $V_p=cste$ : le circuit est un oscillateur harmonique amorti dont la fréquence propre peut être modifiée en faisant varier la constante. Pour vérifier expérimentalement cette propriété, on utilise le montage suivant où un GBF wobulé excite le circuit. On obtient la résonance classique d’un circuit RLC où la fréquence propre est commandée par la constante du signal pompe. 3. Cas où le signal pompe est sinusoïdal :
Considérons le montage de la première figure. L’équation différentielle vérifiée par la tension $V_c$ s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}V_s=kV_pV_c ;\ ;V_s-V_c=ri+L\frac{di}{dt} ;\ ;i=C\frac{dV_c}{dt}\Downarrow\\ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2\left(1-kV_p\right)V_c=0 ;\ ;\omega_0=\frac{1}{\sqrt{LC}} ;\ ;Q=\frac{1}{r}\sqrt{\frac{L}{C}}\\ V_p=0\Rightarrow \underbrace{ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2V_c=0}_{\text{oscillateur harmonique amorti}}\\ V_p=V_{pm}\cos(\omega t)\Rightarrow \underbrace{\frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2(1+h\cos(\omega t))V_c=0}_{\text{equation de Mathieu}} ;\ ;h=-kV_{em}\end{gathered}\right.
3. Cas où le signal pompe est sinusoïdal :
Considérons le montage de la première figure. L’équation différentielle vérifiée par la tension $V_c$ s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}V_s=kV_pV_c ;\ ;V_s-V_c=ri+L\frac{di}{dt} ;\ ;i=C\frac{dV_c}{dt}\Downarrow\\ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2\left(1-kV_p\right)V_c=0 ;\ ;\omega_0=\frac{1}{\sqrt{LC}} ;\ ;Q=\frac{1}{r}\sqrt{\frac{L}{C}}\\ V_p=0\Rightarrow \underbrace{ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2V_c=0}_{\text{oscillateur harmonique amorti}}\\ V_p=V_{pm}\cos(\omega t)\Rightarrow \underbrace{\frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_0^2(1+h\cos(\omega t))V_c=0}_{\text{equation de Mathieu}} ;\ ;h=-kV_{em}\end{gathered}\right.
\end{eqnarray*} La théorie montre ce qui suit :
- Existence de bandes de résonance centrées sur les fréquences $2f_0$, $f_0$, $\frac{2f_0}{3}$,\ldots, $\frac{2f_0}{n},\ ;n\in \mathbb{N}$ où $f_0$ est la fréquence propre du circuit RLC.
- La largeur de chaque bande dépend de l’amplitude du signal excitateur(pompe) $V_{pm}$. Elle est d’autant plus large que l’amplitude est grande.
- La résonance paramétrique a lieu si l’amplitude $V_{pm}$ dépasse un seuil $V_{pm0}$ : $V_{pm}\geq V_{pm0} $.
- Dans le cas de la première bande (celle centrée sur $2f_0$) telle que $V_{pm}$ est très proche du seuil $V_{pm0}$, la tension à la sortie $V_c$ est quasi-sinusoïdale.
- Pour les autres bandes, le signal est très déformé et présente des harmoniques.
\end{eqnarray*} On pose $\omega_1^2=\omega_0^2(1+kE)$ et $\omega_2^2=\omega_0^2(1-kE)$, le système d’équations devient :
\begin{eqnarray*}\left\{\begin{gathered}\frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_1^2V_c=0\\ \frac{d^2V_c}{dt^2}+\frac{\omega_0}{Q}\frac{dV_c}{dt}+\omega_2^2V_c=0\end{gathered}\right.\end{eqnarray*} On suppose que $Q\gg 1$, le système d’équations caractérise deux oscillateurs harmoniques l’un de pulsation propre $\omega_1$ et l’autre $\omega_2$. On cherche des solutions sous la forme : \begin{eqnarray*}\left\{\begin{gathered}V_{c1}=A_1\cos(\omega_1t)+B_1\sin(\omega_1t)\\ V_{c2}=A_2\cos(\omega_2t)+B_2\sin(\omega_2t) \end{gathered}\right.\end{eqnarray*}Les constantes $A_i$ et $B_i$ se déterminent à l’aide des conditions de continuité de $V_c$ et de $\frac{dV_c}{dt}$ en $t=0$. On obtient : $A_1=A_2$ et $B_1\omega_1=B_2\omega_2$ Les deux autres relations de continuité nécessaire à la détermination des constantes s’obtiennent en considérant qu’après chaque période $T_p=\frac{2\pi}{\omega_p}$, $V_c$ et $\frac{dV_c}{dt}$ sont multipliés par une constante $\alpha$ : $V_{c2}\left(\frac{\pi}{\omega_p}\right)=\alpha V_{c1}\left(-\frac{\pi}{\omega_p}\right)\text{ et }\frac{dV_{c2}}{dt}\left(\frac{\pi}{\omega_p}\right)=\alpha \frac{dV_{c1}}{dt}\left(-\frac{\pi}{\omega_p}\right)$Ces conditions impliquent le système suivant : \begin{eqnarray*}\left\{\begin{gathered}A_1\left[\cos\left(\frac{\omega_2\pi}{\omega_p}\right)-\alpha\cos\left(\frac{\omega_1\pi}{\omega_p}\right)\right]+B_1\left[\frac{\omega_1}{\omega_2}\sin\left(\frac{\omega_2\pi}{\omega_p}\right)+\alpha\sin\left(\frac{\omega_1\pi}{\omega_p}\right)\right]=0\\ -A_1\left[\omega_2\sin\left(\frac{\omega_2\pi}{\omega_p}\right)+\alpha\omega_1\sin\left(\frac{\omega_1\pi}{\omega_p}\right)\right]+B_1\left[\omega_1\cos\left(\frac{\omega_2\pi}{\omega_p}\right)-\alpha\omega_1\cos\left(\frac{\omega_1\pi}{\omega_p}\right)\right]=0\end{gathered}\right.\end{eqnarray*} Ce système admet une solution non triviale si son déterminant est nul. Il en résulte l’équation vérifiée par le par le paramètre $\alpha$ sous la forme :
$\alpha^2-2\gamma\alpha+1=0 ;\text{ avec }\quad \gamma=\cos\left(\frac{\omega_1\pi}{\omega_p}\right)\cos\left(\frac{\omega_2\pi}{\omega_p}\right)-\frac{\omega_1^2+\omega_2^2}{2\omega_1\omega_2}\sin\left(\frac{\omega_1\pi}{\omega_p}\right)\sin\left(\frac{\omega_2\pi}{\omega_p}\right)$ Il y a amplification si les racines de l’équation en $\alpha$ sont réelles, c’est à dire : $\Delta>0\Rightarrow \gamma^2>1$. La seule solution qui répond à cette condition est celle donnée par : $\alpha=\gamma+\sqrt{\gamma^2-1} ;\text{ avec }\quad \gamma>1$ L’amplification paramétrique est caractérisée par le fait qu’à chaque période $T_p$, $V_c$ et $\frac{dV_c}{dt}$ sont multipliées par $\alpha>1$. Les non-linéarités du multiplieur limitent la divergence de $V_c$ : ainsi la résonance paramétrique correspond à une instabilité du système.
Expérience en vidéo
Le signal pompe est un signal continu
Expérience en vidéo
Le signal pompe est un signal continu
[download id="4907"]
Expérience en vidéo
Le signal pompe est un signal sinusoïdal
Expérience en vidéo
Le signal pompe est un signal sinusoïdal
[download id="4919"]
Expérience en vidéo
signal pompe sinusoïdal : bandes de résonance paramétrique
Expérience en vidéo
signal pompe sinusoïdal : bandes de résonance paramétrique
[download id="4928"]
Expérience en vidéo
Le signal pompe est un signal carré
Expérience en vidéo
Le signal pompe est un signal carré
