• Mise en évidence expérimentale de la résonance magnétique nucléaire
• Détermination du rapport gyromagnétique $\gamma$ des différentes substances

Montage expérimental

Dispositif RMN

• Module RMN+échantillons
• Oscilloscope numérique
• Carte d’acquisition+PC

1. Principe de la spectroscopie RMN La spectroscopie de résonance magnétique nucléaire est une technique d’analyse chimique. Elle permet d’apporter une information précise et individuelle sur la très grande majorité des atomes constitutifs de la molécule, d’identifier les connexions entre atomes des diverses entités. Elle est largement utilisée dans des domaines variés :

• En chimie : la technique apporte des informations sur la structure, les mouvements et les réactions chimiques des molécules, mais aussi sur les dynamiques d’échange,
• en physique du solide : la technique permet d’extraire les informations structurales détaillées : environnement chimique local, degré de distorsion des polyèdres, nombre de sites et multiplicités relatives dans le cas des cristaux,
• en biologie : la RMN a permis de faire des progrès considérables dans la connaissance des macromolécules. Elle a revolutionné le diagnostic médical et a permis de visualiser en trois dimensions la concentration en eau de la matière molle (tissu biologique, muscles,$\ldots$)

Son principe de fonctionnement repose sur l’interaction entre un champ magnétique et un moment magnétique permanent d’origine nucléaire dû à son spin (I). Lorsqu’on applique un champ magnétique statique selon Oz par exemple la levé de dégénérescence permet au moment magnétique associé au moment cinétique de spin d’avoir deux configurations dans le cas où le spin nucléaire est égal à $I=\frac{1}{2}$ :

• le moment magnétique $\overrightarrow \mu $ est un vecteur sur un cône autour de l’axe Oz. Sa composante selon Oz est $-\frac{\gamma\hbar}{2}$, où $\gamma$ est le rapport gyromagnétique. Cette configuration lui correspond une énergie $\varepsilon_+=-\overrightarrow \mu\cdot\overrightarrow B=\frac{+\gamma\hbar B_{st}}{2}$.
• le moment magnétique est situé sur le cône autour de l’axe Oz, orienté vers $+\overrightarrow e_z$, telle que sa composante selon Oz est $\frac{\gamma\hbar}{2}$. Cette configuration lui correspond une énergie $\varepsilon_-=-\overrightarrow \mu\cdot\overrightarrow B=\frac{-\gamma\hbar B_{st}}{2}$

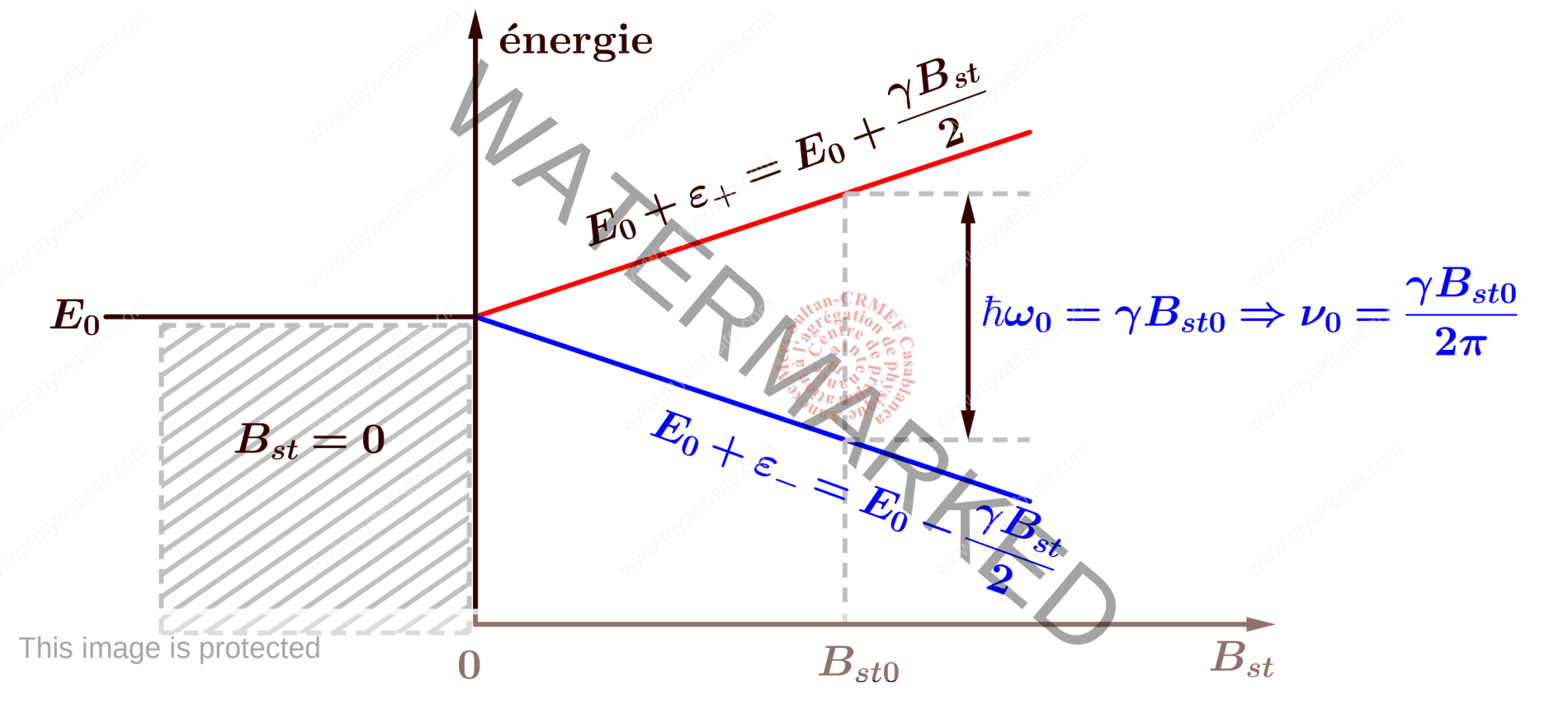
Des transitions entre ces états sont possibles par absorption ou émission d’une onde électromagnétique dont la fréquence $\nu$ est telle que $h\nu=\gamma\hbar B_{st}$. La technique consiste à appliquer un champ magnétique radiofréquence de faible amplitude se trouvant dans un plan perpendiculaire au champ statique utilisé pour lever la dégénérescence(effet Zeeman). La mesure de la fréquence de transition permet d’obtenir des informations structurales importantes locales.2. Pourquoi on applique un champ magnétique radiofréquence perpendiculaire au champ statique ? Les états quantiques séparés énergitiquement par effet Zeeman sont notés comme suit : l’état de basse énergie $\varepsilon_-$ est noté par $|a\rangle$ et l’état d’énergie $\varepsilon_+$ est noté par $|b\rangle $. Le moment magnétique $\overrightarrow \mu$ proportionnel au moment cinétique de spin $\overrightarrow I$ est quantifié : $\widehat{\overrightarrow \mu}=\gamma\widehat{\overrightarrow I}$ où $\gamma$ est le rapport gyromagnétique. Le moment magnétique de transition entre ces états est donné par : $$\widehat{\overrightarrow \mu}_{ab}=\langle a|\widehat{\overrightarrow \mu}|b\rangle$$ L’interaction a lieu entre le moment magnétique de transition et le champ magnétique radiofréquence $\overrightarrow B_{rf}=\overrightarrow B_{rf}\cos(\omega t)$. L’hamiltonien d’intéraction s’exprime sous la forme : $$\widehat H=-\widehat{\overrightarrow \mu}_{ab}\cdot \overrightarrow B_{rf}=-\gamma[\langle a|\widehat I_x|b\rangle B_{rfx}+\langle a|\widehat I_y|b\rangle B_{rfy}+\langle a|\widehat I_z|b\rangle B_{rfz}]\cos(\omega t)$$ Les états $|a\rangle$ et $|b\rangle$ sont deux vecteurs propres ohrtogonaux de $\hat I_z$. Il en résulte que $\langle a|\hat I_z|b\rangle =0$. Par suite, seules les composantes selon $Ox $ et  $Oy$ du champ magnétique radiofréquence interviennent dans l’expression de l’hamiltonien d’interaction(le moment magnétique de transition n’a pas de composante selon Oz). Cette propriété peut être obtenue à l’aide d’une analyse classique : le moment magnétique effectue un mouvement de précession autour du champ magnétique statique, c’est à dire selon Oz. Il en résulte que la composante du moment magnétique selon Oz reste constante et les composantes selon Ox et Oy oscillent à la pulsation de Larmor $\omega_L=\gamma B$. Les composantes du moment magnétique dans le plan perpendiculaire au champ magnétique statique représentent le moment magnétique de transition défini en description quantique. La résonance a lieu lorsque la fréquence radiofréquence s’identifie avec la fréquence de Larmor.3. Quel est la grandeur macroscopique associée à l’interaction du champ magnétique avec les spins nucléaires ? La grandeur macroscopique qui intervient c’est l’aimantation puisque le champ magnétique interagit avec un ensemble de spin nucléaire. L’application d’un champ magnétique statique lève la dégénérescence par effet Zeeman et conduit à un système à deux niveaux pour le cas du spin $\frac{1}{2}$. À l’équilibre thermique, les moments magnétiques sont répartis selon une distribution de Boltzmann. La somme des moments magnétiques donne une aimantation alignée sur le champ statique. L’aimantation résultante est proportionnelle au rapport des populations des deux niveaux : $$M\propto \frac{N_{\alpha}}{N_{\beta}}\propto \exp\left(\frac{\gamma B_{st}}{k_BT}\right)\propto \exp\left(\frac{h\nu_0}{k_BT}\right)$$ Ordres de grandeurs : $B_{st}=1\ ;T$ ; $\nu_0=42,58 \ ;MHz$ ; T=300 K ; $k_B=1,38.10^{-23}\ ;S.I.$ : $$\exp\left(\frac{\gamma B_{st}}{k_BT}\right)=\exp\left(\frac{h\nu_0}{k_BT}\right)=1.0000068$$ L’écart entre les polpulations des deux niveaux est très faible. 
 C’est pour cette raison on utilise des champs statiques intenses.4. Quels sont les noyaux qui peuvent donner un signal RMN ?

5. Spin nuècléaire $I>\frac{1}{2}$ : élargissement des raies Lorsque le spin nucléaire I est supérieur à 1/2, la levé de dégénérescence conduit à 2I+1 niveaux, ce qui a pour effet d’élargir les raies RMN. Pour un spin demi-entier, on obtient une raie centrale correspondante à la transition entre $m_I=-\frac{1}{2}$ et $m_I=\frac{1}{2}$ et des raies satellites correspondantes aux transitions $\Delta m_I=\pm 1$.5.1. Propriétés d’un spectre RMN Un signal RMN est caractérisé par :

• la position : elle est définie par le déplacement chimique $\delta$. Chaque noyau possède un environnement chimique qui lui est propre. Ceci est dû au fait que le champ statique appliqué induit des courants dans les nuages électroniques autour des noyaux. Ces courants induisent des champs magnétiques dans le sens opposé. Le champ présenti par le noyau peut s’écrire sous la forme $B_{eff}=B_{st}(1-\sigma)$, où $\sigma$ set la constante d’écran qui dépend de l’environnement local. La fréquence à appliquer est une caractéristique de l’environnement local.
• la forme est en général une lorentzienne. L’intensité des raies correspond à l’aimantation macroscopique qui est proportionnelle au rapport des populations des deux niveaux mises en jeu dans le cas d’un spin nucléaire 1/2 : $$M\propto\exp\left(\frac{\hbar\gamma B_{st}}{k_BT}\right)$$ L’écart énergétique, lié à l’intensité de la raie, dépend du noyau étudié puisque elle est proportionnelle au rapport gyromagnétique. Ainsi, les noyaux ayant un rapport gyromagnétique $\gamma$ élevé sont plus faciles à analyser : c’est le cas pour $^1_1H$, $^{19}_9F$ et $^{31}_{15}P$. L’intensité dépend également de l’abondance naturelle du noyau.

   L’air du signal, obtenu par intégration, permet de remonter au nombre de spins impliqués dans la transition associée au signal RMN.

• l’interaction avec le champ radiofréquence appliqué,
• l’interaction par déplacement chimique dépend de l’environnement du noyau. Dans ce cas, le champ effectif ressenti par le spin nucléaire est donné par : $$\overrightarrow B_{eff}=\overrightarrow B_{st}(1-\sigma) ;\quad\sigma=\begin{pmatrix}\sigma_1&0&0\\0&\sigma_2&0\\0&0&\sigma_3\end{pmatrix}$$ où $\sigma$ est la constante d’écran.
• par couplage dipolaire : c’est l’interaction spin-spin ou dipôle-dipôle. Elle est proportionnelle au produit des rapport gyromgnétiques des deux spins.

• par couplage scalaire : c’est une interaction entre spins à travers les électrons des liaisons
• par couplage quadrupolaire pour les noyaux dont le spin I est supérieur à $1/2$ : les spins nucléaires $>1/2$ sont caractérisés par une distribution des charges non sphérique. Il en résulte un moment quadrupolaire qui interagit avec le champ électrique local créé par la distributions des charges électriques proche du noyau

• la relaxation longitudinale due à l’interaction spin-réseau. Elle est caractérisé par un temps de relaxation $\tau_L$
• la relaxation transversale. Elle est due à l’interaction spi-spin et caractérisée par un temps de relaxation $\tau_T$. C’est le temps que mettent les spin pour perdre leur cohérence de phase.

• la RM utilisée actuellement dans le domaine de la recherche et de l’industrie est dite à impulsion : le champ magnétique statique $B_{st}$ est fixe. À partir de l’équilibre thermodynamique on fait basculer les moments magnétiques sur une direction du plan perpendiculaire au champ magnétique statique grâce à une impulsion radiofréquence. Le transformée de fourrier du signal fournit le spectre RMN de l’échantillon.
• Dans la version didactique la RMN est dite à onde continue où on fait varier lentement le champ magnétique statique jusqu’à ce que la condition de résonance soit satisfaite.