Obtenir la courbe de résonance [peekaboo_content]   de différente manières :

• à l’aide de la détection de crête sans seuil,
• à l’aide de la détection numérique d’enveloppe faisant intervenir la transformée de Hilbert,
• à l’aide de la réponse impulsionnelle,
• à l’aide de la réponse indicielle.

[/peekaboo_content]

Montage expérimental(courbes de résonance à l’aide de la détection de crête sans seuil)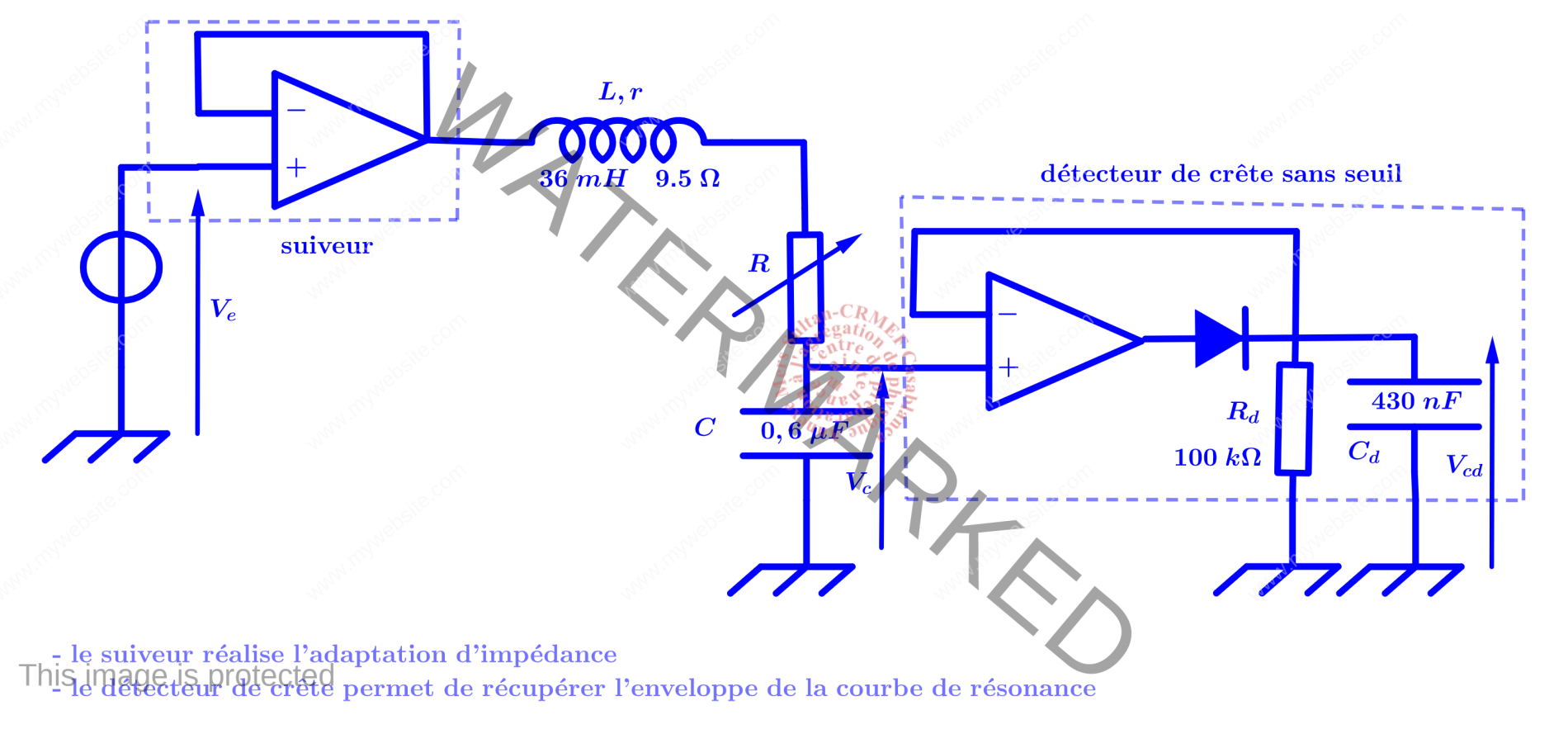

[peekaboo_content]Montage expérimental(détection numérique d’enveloppe,  réponse impulsionnelle et réponse indicielle)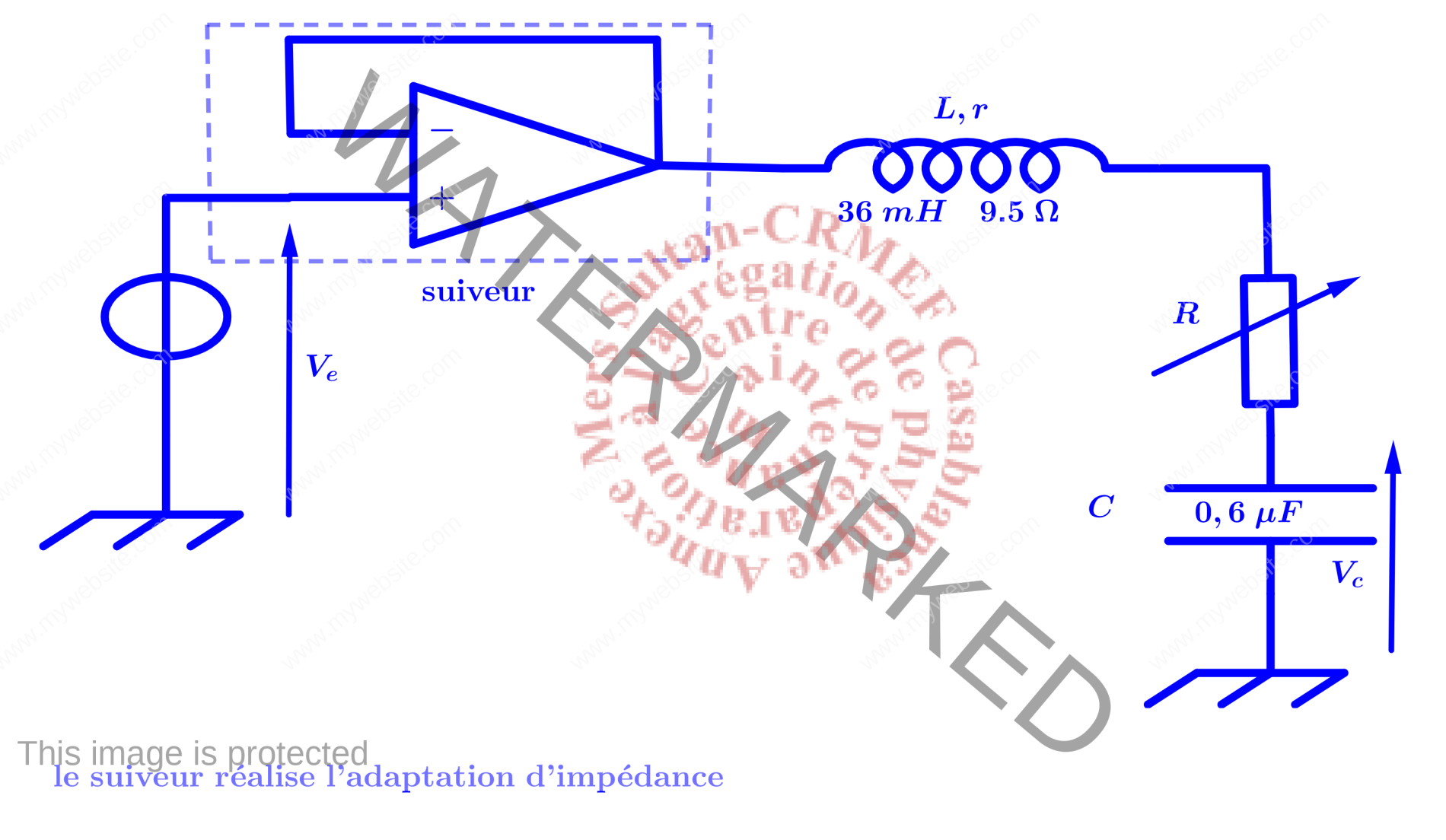[/peekaboo_content]

1. Courbe de résonance en tension à l’aide de la détection de crête sans seuil Considérons le montage de la figure ci-dessous. On se place en régime sinusoïdal forcé. L’amplitude complexe de la tension aux bornes de la capacité $V_c$ s’obtient comme suit : \begin{eqnarray*}\left\{\begin{gathered}\underline V_e=jL\omega\underline I+(r+R)\underline I+\underline V_c ;\quad \underline I=j\omega C\underline V_c\Downarrow\\\underline V_c=\frac{\underline V_e}{1-\frac{\omega^2}{\omega_0^2}+j\frac{\omega}{\omega_0Q}} ;\quad \omega_0^2=\frac{1}{LC} ;\quad Q=\frac{L\omega_0}{R+r}=\frac{1}{C\omega_0(R+r)}\\x=\frac{\omega}{\omega_0}\Rightarrow |\underline V_c|=\frac{|\underline V_e|}{\sqrt{(1-x^2)^2+\frac{x^2}{Q^2}}}\\\frac{d|\underline V_c|}{dx}=0\Rightarrow x=\sqrt{1-\frac{1}{2Q^2}} ;\quad Q\geq \frac{1}{\sqrt{2}}\end{gathered}\right.\end{eqnarray*}Ainsi la résonance n’aura lieu que si $Q\geq\frac{1}{\sqrt{2}}$. La pulsation de résonance est $\omega_{res}=\omega_0\sqrt{1-\frac{1}{2Q^2}}$ et ne coïncide avec la pulsation propre que si Q est important. Lorsqu’on augmente R, le facteur de qualité diminue, ce qui se traduit par la diminution de la pulsation de résonance. \noindent Pour obtenir la courbe de résonance, la tension $V_e$ est un signal sinusoïdal dont la fréquence varie lentement avec le temps selon la forme : \begin{eqnarray*}f_{\text{instantanee}}=f_{start}+\frac{f_{stop}-f_{start}}{\text{duree}}t\end{eqnarray*}Le détecteur de crête est constitué de deux blocs. L’ampli. Op. et la diode constituent le premier bloc et permettent d’éliminer la partie négative du signal $V_c$. Le deuxième bloc, constitué de $R_d$ et $C_d$, combiné au premier bloc, permet de récupérer l’enveloppe par la charge du condensateur lorsque la diode conduit et la décharge à travers $R_d$ lorsque la diode est bloquée à condition de choisir $R_dC_d\gg T_{start}=\frac{1}{f_{start}}$ [peekaboo_content]2. Courbes de résonance à l’aide de la détection numérique d’enveloppe faisant intervenir la transformée de Hilbert 2.1. Principe de la transformée de Hilbert 2.1.1. Définition et propriétésLa transformée de Hilbert $H(x(t))=\widetilde{x}(t)$ d’une fonction réelle x(t) est définie par :\begin{eqnarray*}\widetilde{x}(t)=f(t)\otimes\frac{1}{\pi t}=\frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{x(\tau)}{t-\tau}d\tau\end{eqnarray*}où $\otimes$ représente le produit de convolution. En raison d’une singularité possible à $t = \tau$, l’intégrale doit être considérée comme la valeur principale de Cauchy : \begin{eqnarray*}\widetilde{x}(t)=\frac{1}{\pi}\lim\limits_{\varepsilon \rightarrow 0} \left\{\int_{-\infty}^{-\varepsilon}\frac{x(\tau)}{t-\tau}d\tau+\int_{+\varepsilon}^{+\infty}\frac{x(\tau)}{t-\tau}d\tau\right\}\end{eqnarray*}La transformée de Hilbert peut être interprétée comme un filtre linéaire invariant dans le temps. Sa réponse impulsionnelle s’exprime par :\begin{eqnarray*} h(t)=\widetilde{\delta(t)}=\frac{1}{\pi t}\otimes \delta(t)=\frac{1}{\pi t}\end{eqnarray*}La fonction de transfert de ce filtre (transformée de Fourier de la réponse impulsionnelle) est donnée par :\begin{eqnarray*} H(\omega)=-j \rm sign(\omega)\end{eqnarray*}où $\rm sign$ représente la fonction signe :\begin{eqnarray*} \rm sign(x)=\left\{\begin{gathered}+1\text{ si }x>0\\ -1\text{ si }x<0\end{gathered}\right.\end{eqnarray*}et $j$ le nombre complexe $j^2=-1$. Il s’agit d’un filtre passe-tout déphaseur de $-\frac{\pi}{2}$. \noindent La transformée de Hilbert d’une fonction x(t) est sous forme d’un produit de convolution. Il en résulte que pour la calculer, il suffit de calculer la transformée de Fourier inverse du produit de la transformée de Fourier $X(\omega)$ par la fonction de transfert $H(\omega)=\rm -jsign(\omega)$ : \begin{eqnarray*} \widetilde{x}(t)=\mathcal F^{-1}(\rm H(\omega)\times X(\omega)) =\mathcal F^{-1}(\rm-jsign(\omega)\times X(\omega)) \end{eqnarray*} La transformée de Hilbert vérifie les propriétés suivantes :

• linéarité : la transformée de Hilbert d’une somme est la somme des transformées de Hilbert.\begin{eqnarray*}\forall \lambda_1 \ ;\rm et\ ;\lambda_2\in\mathbb C,\widetilde{\lambda_1x_1(t)+\lambda_2x(t)}=\lambda_1\widetilde{x_1}(t)+\lambda_2\widetilde{x_2}(t) \end{eqnarray*}
• La transformée de Hilbert du produit d’une fonction basse fréquence $x_{BF}(t)$ et une fonction haute fréquence $y_{HF}(t)$ dont les spectres respectifs dont disjoints est donné par l’identité de Bedorsian : \begin{eqnarray*}\rm \widetilde{x_{BF}(t)y_{HF}(t)}=x_{BF}(t)\widehat{y_{HF}(t)}\end{eqnarray*}

2.2. Utilité pratique : extraction de l’enveloppe et de la phase On s’intéresse dans toute la suite aux signaux à bande étroite. 2.2.1. Signal analytiqueSoit un signal réel x(t) de transformée de Fourier $X(f)$. Le signal analytique correspondant a(t) est définit par : \begin{eqnarray*} a(t)=x(t)+j\widetilde{x}(t) \end{eqnarray*} Le signal réel est la partie réelle du signal analytique associé $x(t)=\mathcal{R}e(a(t))$. La transformée de Fourier du signal analytique s’exprime sous la forme : \begin{eqnarray*} A(f)=X(f)+\rm sign(f)X(f)=\left\{\begin{gathered}2X(f)\text{ si }f>0\\0\text{ si }f<0\end{gathered}\right. \end{eqnarray*} Le spectre du signal analytique s’identifie avec celui du signal réel dans le domaine des fréquences positives à un facteur de 2 près. 2.2.2. Enveloppe complexeEn général, le spectre du signal analytique est centrée autour d’une fréquence $f_0$. On définit l’enveloppe complexe y(t) d’un signal réel à bande étroite le signal y(t) dont la transformée de Fourier Y(f) identique au spectre du signal analytique mais centré sur 0 : \begin{eqnarray*} Y(f)=A(f+f_0)\Rightarrow y(t)=a(t)\exp(-j2\pi f_0t) \end{eqnarray*} L’enveloppe complexe possède comme module $|y(t)|$ et d’argument $arg(y(t))$. Il en résulte l’expression du signal réel à bande étroite : \begin{eqnarray*} x(t)=\mathcal Re(a(t))=|y(t)|\cos(2\pi f_0t+\rm arg(y(t))) \end{eqnarray*} l’enveloppe complexe est un signal basse fréquence de variation lente par rapport à $f_0$. Le signal réel est un signal sinusoïdal de fréquence $f_0$ et d’amplitude $|y(t)|$ lentement variable. Ces caractéristiques sont données par :

• l’amplitude instantanée : $|y(t)|$,
• la phase instantanée : $\Psi(t)=2\pi f_0 t+\rm arg(y(t))$
• la fréquence instantanée : $f(t)=\frac{1}{2\pi}\frac{d\Psi(t)}{dt}=f_0+\frac{1}{2\pi}\frac{d\rm arg(y(t))}{dt}$

2.3. Montage expérimentale Le montage expérimental est donnée dans la figure ci-dessous. Le GBF délivre un signal sinusoïdal dont la fréquence varie de manière linéaire entre deux fréquences $f_{start}$ et $f_{stop}$ durant une durée $\Delta t$. L’expression de l’amplitude complexe est donné dans le paragraphe ci-dessus. 3. Courbes de résonance à l’aide de la réponse impulsionnelle 3.1. Principe de la réponse impulsionnelle Toute fonction x(t) s’exprime à l’aide de la distribution de Dirac $\delta$ sous la forme :\begin{eqnarray*}\label{conv} x(t)=\int_{-\infty}^{+\infty}x(\tau)\delta(t-\tau)d\tau=x(t)\otimes\delta(t)\end{eqnarray*}Il s’agit d’un produit de convolution de x(t) par delta(t). Considérons un filtre linéaire et invariant dans le temps (un retard à l’entrée se manifeste par un retard identique à la sortie sans changer la forme). Soit s(t) la réponse à une entrée e(t). La réponse impulsionnelle h(t) est définie par sa réponse à une impulsion de Dirac, c’est à dire : \begin{eqnarray*}e(t)=\delta(t)\Rightarrow s(t)=h(t)=R(\delta(t))\end{eqnarray*}où R est un opérateur linéaire.\noindent Un signal quelconque e(t) est une somme infinie d’impulsions décalées. Chacune de ces impulsions engendre une sortie sous forme d’une réponse impulsionnelle décalée (le système est invariant dans le temps). Le système est linéaire, la réponse à la somme des impulsions décalées est la somme des réponses à chaque impulsion : \begin{eqnarray*}s(t)=R(e(t))=\int_{-\infty}^{+\infty}e(\tau)h(t-\tau)d\tau=e(t)\otimes h(t)\end{eqnarray*}La causalité impose une condition sur h(t) de la forme   : \begin{eqnarray*}h(t)=0\text{ si } t<0\Rightarrow s(t)=\int_{-\infty}^t x(\tau)h(t-\tau)d\tau\end{eqnarray*}\begin{eqnarray*}h(t)=0\text{ si } t<0\Rightarrow s(t)=\int_{-\infty}^t x(\tau)h(t-\tau)d\tau\end{eqnarray*}La relation entrée-sortie est un produit de convolution entre l’entrée et la réponse impulsionnelle du filtre dans le domaine temporel. La transformée de Fourier de cette relation s’exprime par : \begin{eqnarray*}\widehat S(f)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}h(t-\tau)e(\tau)\exp(-j2\pi ft)d\tau dt\end{eqnarray*}En effectuant le changement de variable $t-\tau=u$  on obtient l’expression de la transformée de Fourier de la sortie sous la forme : \begin{eqnarray*}\widehat S(f)=\widehat H(f)\times \widehat E(f)\end{eqnarray*}Ainsi la relation entrée-sortie dans le domaine fréquentiel se manifeste par le produit de la transformée de Fourier de l’entrée qui est égale à 1(impulsion de Dirac) et de la fonction de transfert $H(f)$. La courbe de résonance représente le module de la fonction de transfert. Celle-ci est la transformée de Fourier de la réponse impulsionnelle du filtre. 3.2. Montage expérimental Le montage est celui du paragraphe précédent. Dans ce cas le GBF délivre des impulsions périodiques de période T très grande devant la durée $\tau $ de l’impulsion qui est très petite devant la pseudo-période du circuit. L’amplitude complexe de la tension $V_c$ est donnée dans le premier paragraphe. 4. Courbes de résonance à l’aide de la réponse indicielle 4.1. Principe de la réponse indicielle La réponse indicielle est la réponse à un échelon de tension $v_e(t) $ de la forme : \begin{eqnarray*}v_e=\left\{\begin{gathered}E\text{ si } t>0\\ 0\text{ si } t<0\end{gathered}\right.\end{eqnarray*}Soit $s_e(t)$ la réponse du système à l’échelon de tension $v_e$.  Celle-ci vérifie les deux relations suivantes : \begin{eqnarray*}s_e(t)=\int_{-\infty}^{+\infty}v_e(\tau)h(t-\tau)d\tau\Leftrightarrow S_e(f)=H(f)\times V_f(f)\end{eqnarray*}où les symboles en majuscules représentent les transformées de Fourier des grandeurs. Lorsque $v_e=v_i=E\delta(t)$, la sortie est $s_i(t)=h(t)$. La dérivée au sens des distributions de l’échelon de tension $v_e$ est donnée par  $E\delta(t)$. La transformée de Fourier de la dérivée de la réponse indicielle $s_e(t)$ est donnée par : \begin{eqnarray*}TF\left(\frac{ds_e(t)}{dt}\right)=j\omega S_e(\omega)=j\omega V_e(\omega)H(\omega)\end{eqnarray*}3.2. Montage expérimental Le montage est celui utilisé dans le deuxième paragraphe. Dans ce cas le GBF délivre un signal rectangulaire de rapport cyclique $50\