• Allure de la résistivité électrique du germanium non dopé en fonction de la température,
• détermination de l’énergie du gap du germanium.

Montage expérimental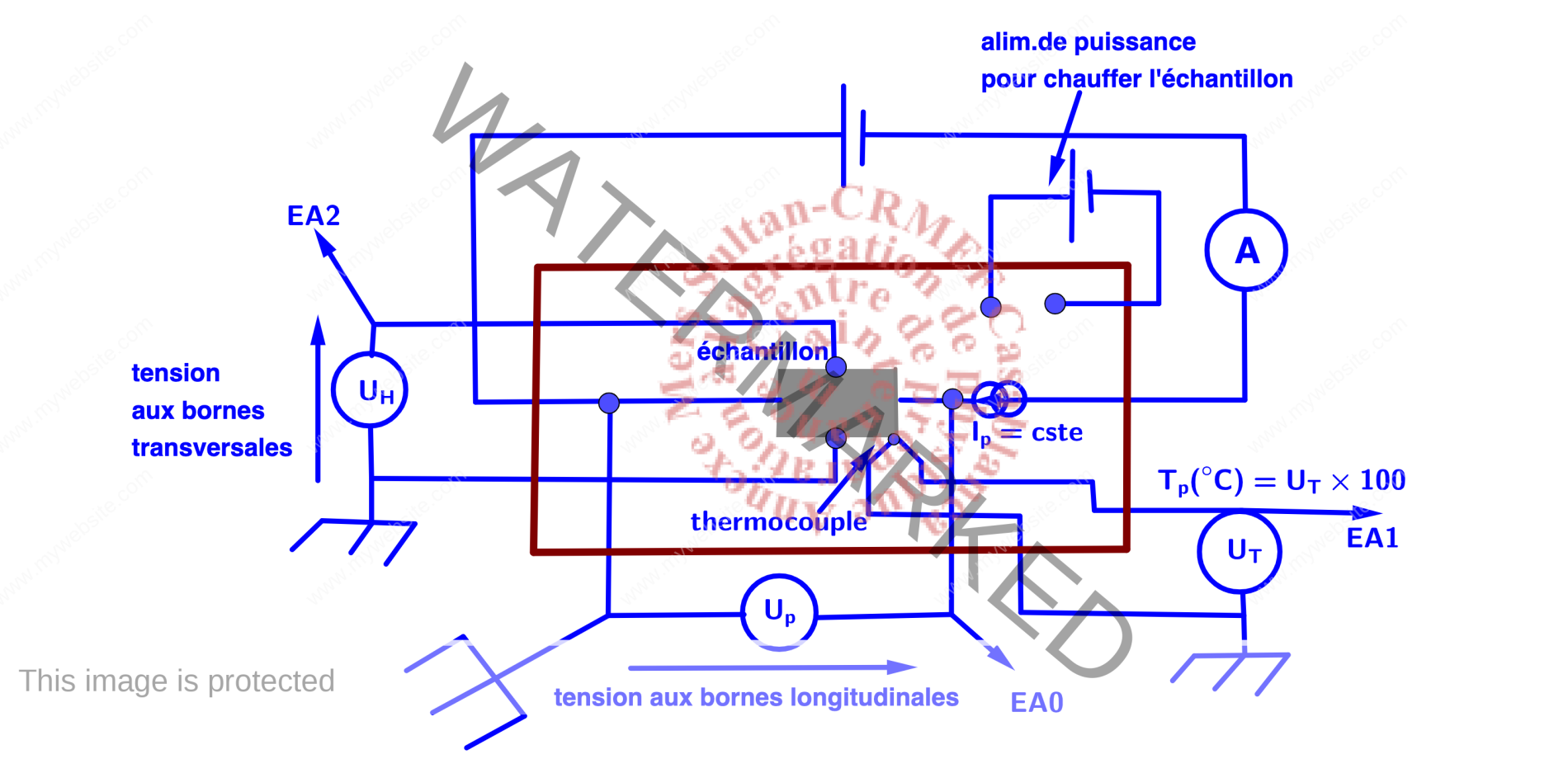

• Console à effet Hall avec son alimentation(transformateur-redresseur)
• Alimentation stabilisée de puissance,
• platine avec cristal de germanium non dopé,
• capteur de champ magnétique à effet Hall,
• bobines  avec noyau en U,
• multimètres,
• Carte d’acquisition+PC
• fils électriques.

1. Définition d’un semi-conducteur Un semiconducteur est un matériau caractérisé par une résistivité électrique $\rho$ très inférieure à celle des isolants et très grande par rapport à celle des conducteurs :
$10^{-5}\,\Omega.cm^{-1}\ll \rho \ll 10^{8}\,\Omega.cm^{-1}$. Une plage de $\rho(\Omega.cm^{-1})$ peut être : $\rho \in[10^{-3}, 10^{4}]$.

Un semiconducteur intrinsèque est un semiconducteur pur dépourvu de tous défauts résiduels

2. Propriéts conductrices d’un semiconducteur 2.1. Réseau direct Les cristaux sont constitués d’un empilement d’entités atomiques ioniques ou moléculaires selon un arrangement régulier dans l’espace.  

• on représente les centres des édifices chimiques par des points.  
• l’ensemble des points obtenu est appelé réseau direct.
• Chaque point du réseau est appelé nœud.  
• $\exists (\overrightarrow a, \overrightarrow{b}, \overrightarrow{c})$non coplanaire tel que $\forall $ le point M par rapport à un nœud situé en O :  $\overrightarrow{OM}=n\overrightarrow a+m\overrightarrow b+p\overrightarrow c ;\,\,m,n,p\in \mathcal Z$
• La maille élémentaire est définie par ses trois vecteurs $(\overrightarrow a,\overrightarrow b, \overrightarrow c)$. Son volume est : $V_d=\overrightarrow a\cdot(\overrightarrow b\wedge \overrightarrow c)$

• Le réseau réciproque est l’ensemble des points $\overrightarrow{K}$ tels que : \begin{align*}\overrightarrow{K}=m^*\overrightarrow{A}+n^*\overrightarrow{B}+p^*\overrightarrow{C} ;\,\,m^*,n^*,p^*\in\mathcal Z\\\overrightarrow{A}=2\pi\frac{\overrightarrow{b}\wedge \overrightarrow{c}}{\overrightarrow{a}\cdot(\overrightarrow{b}\wedge \overrightarrow{c})} ;\,\overrightarrow{B}=2\pi\frac{\overrightarrow{c}\wedge \overrightarrow{a}}{\overrightarrow{a}\cdot(\overrightarrow{b}\wedge \overrightarrow{c})} ;\,\overrightarrow{C}=2\pi\frac{\overrightarrow{a}\wedge \overrightarrow{b}}{\overrightarrow{a}\cdot(\overrightarrow{b}\wedge \overrightarrow{c})}\\\overrightarrow A\cdot\overrightarrow{a}=2\pi ;\,\overrightarrow B\cdot\overrightarrow{b}=2\pi ;\,\overrightarrow C\cdot\overrightarrow{c}=2\pi ;\,\end{align*}
• $(\overrightarrow{A},\overrightarrow{B},\overrightarrow{C})$ constituent les vecteurs de base du réseau réciproque.
• Le volume de la maille élémentaire du réseau réciproque est donné par : $V_r=\overrightarrow{A}\cdot(\overrightarrow{B}\wedge \overrightarrow{C})$
• L’intérêt du réseau réciproque se situe au niveau du fait que la figure de diffraction des rayons X renvoie l’image du réseau réciproque ou espace de Fourier

• On suppose que les ions sont fixes(plus lourds que les électrons)
•   On considère chaque électron en mouvement dans un potentiel périodique dû à tous les autres électrons du réseau. On réduit alors le problème à N électrons indépendants.

Cette expression traduit le théorème de Bloch

2.5. Conséquences du théorème de Bloch : première zone de Brilloin On considère le cas d’une chaîne à N sites. N valeurs sont possibles pour k tels que : $k=\frac{p}{N}\frac{2\pi}{a} ;\,p\text{entier}$ Supposons que $p>N$, il existe deux entiers m et l tels que $p=mN+l\Rightarrow \overrightarrow k=m\frac{2\pi}{a}\overrightarrow e_x+\frac{l}{N}\frac{2\pi}{a}\overrightarrow e_x=\overrightarrow G+\overrightarrow k_b$ où $\overrightarrow G$ est un vecteur du réseau réciproque. La relation entre $\psi_k(x)$ et $\psi_{k_1}(x)$ s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}\psi_k(x+pa)=\exp(ikpa)\psi_k(x)=\exp(ik_bpa)\psi_k(x) ;\quad\exp(iGpa)=1\\\psi_{k_b}(x+pa)=\exp(ik_bpa)\psi_{k_b}(x)\end{gathered}\right.\Rightarrow \psi_k(x)=\psi_{k_b}(x)\end{eqnarray*}Les énergie propres $\varepsilon(\overrightarrow k)$ sont invariantes pour toute translation d’un vecteur du réseau réciproque $\varepsilon(\overrightarrow k+\overrightarrow G)=\varepsilon(\overrightarrow k)$.  

Conclusion : k peut être choisi dans la maille élémentaire du réseau réciproque. Il est commode de le choisir dans la maille de Wigner-Seitz.

2.6. Importance de la zone de Brilloin : représentation des bandes d’énergie C’est une maille du réseau réciproque ayant le volume d’une maille élémentaire $(\overrightarrow{A},\overrightarrow{B},\overrightarrow{C})$. Elle est formée de l’ensemble des points qui sont les plus proches d’un point  $G_0$ par exemple origine que de n’importe quel autre point G. Pour la tracer on procède comme suit : 

•  On trace les plans bissecteurs des vecteurs joignant $G_0$ à $G$ quelconque du réseau réciproque 
• la première zone de Brillouin est appelée cellule de Wigner-Seitz du réseau réciproque. Elle possède toutes les propriétés du cristal.

2.7. Bandes d’énergie : modèle de Kronig-Penney

• On représente le potentiel créé par une chaîne linéaire de N atomes $(N\gg 1)$ par un potentiel périodique en créneaux
• Les solutions de l’équation de Schrödinger dans les régions (I) et (II) sont données par : \begin{eqnarray*}\phi_{II}(x)=A\exp(i\alpha x)+B\exp(-i\alpha x) ;\quad \alpha^2=\frac{2mE}{\hbar^2}\\\phi_{I}(x)=C\exp(\beta x)+D\exp(-\beta x) ;\quad \beta^2=\frac{2m(V_0-E)}{\hbar^2} ;\,V_0>E\end{eqnarray*}
• les paramètres A, B, C et D se déterminent à l’aide des conditions de continuité de la fonction d’onde de Bloch et de sa dérivée. La fonction d’onde vérifie le théorème de Bloch :  $\phi(x+a+b)=\exp(ik(a+b))\phi(x)$

• Continuité en x=0 et en x=a : \begin{eqnarray*}\left\{\begin{gathered}\phi_I(0)=\phi_{II}(0)\Rightarrow C+D=A+B\\\phi’_I(0)=\phi’_{II}(0)\Rightarrow \beta(C-D)=i\alpha(A-B)\\\phi_{II}(a)=\phi_{III}(a)=\phi_I(-b)\exp(ik(a+b))\Downarrow\\ A\exp(i\alpha a)+B\exp(-i\alpha a)=\exp(ik(a+b)))[C\exp(-\beta b)+D\exp(\beta b)]\\\phi’_{II}(a)=\phi’_{III}(a)=\phi’_I(-b)\exp(ik(a+b))\Downarrow\\i\alpha[A\exp(i\alpha a)+B\exp(-i\alpha a)]=\exp(ik(a+b))\beta[C\exp(-\beta b)-D\exp(\beta b)]\end{gathered}\right.\end{eqnarray*}
• on obtient un système de 4 équations à 4 inconnues. Celui-ci possède une solution non nulle si le déterminant est nul.

• On obtient l’équation de dispersion suivante : $\cos(k(a+b))=\frac{\beta^2-\alpha^2}{2\alpha\beta}\sin(\alpha a)\sin(\beta b)+\cos(\alpha a)\cos(\beta b)$
• Kronig et Penny on fait tendre la barrière vers l’infini et b vers 0(pic de Dirac) tel que $bV_0=cste$. L’équation se simplifie et devient : $\cos(ka)=\cos(\alpha a)+P\sin c(\alpha a) ;\,P=\frac{mV_0ba}{\hbar^2}$.

  La résolution numérique, avec P un paramètre, montre l’existence de bandes d’énergie comme le montre la simulation Géogebra.

2.8. Approximation des électrons quasilibres

•   On considère une chaîne de N atomes identiques équidistants de a le long de l’axe Ox et de longueur L=Na.
• Dans le cas où l’électron est libre, l’hamiltonien est $H_0=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}$ et l’énergie est $\varepsilon^0(k)=\frac{\hbar^2k^2}{2m}$
• Le potentiel périodique est très faible par rapport à l’énergie de l’électron libre. Son effet est traité comme une perturbation. On suppose que le développement  en série de Fourier de V(x) s’exprime par : $V(x)=\sum_mV_m\exp\left(im\frac{2\pi}{a}x\right) ;\ ;V_0=0$
• Dans ce cas l’hamiltonien devient : $H=H_0+V(x)$. L’énergie est une fonction paire de k : il y a une dégénérescence dans les sous espace (k,-k). L’hamiltonien possède comme matrice : $H=\begin{pmatrix}\varepsilon^0(k)+V_{k,-k}&V_{k,-k}\\ V_{-k,k}&\varepsilon^0(-k)+V_{-k,-k}\end{pmatrix}$ 

•   \begin{eqnarray*}V_{k,k}=V_{-k,-k}=0 ;\quad V_{-k,k}=V_{k,-k}\\ V_{k,-k}=\frac{1}{L}\sum_{m\neq 0}\int_0^L\exp(-ikx)V_m\exp\left(im\frac{2\pi x}{a}\right)\exp(-ikx)\neq 0\text{ si }2k=p\frac{2\pi}{a} ;p\text{ entier}\end{eqnarray*}
•   Pour $k=\pm \frac{\pi}{a}$ on diagonalise l’hamiltonien pour déterminer les valeurs de l’énergie : $\left|\begin{matrix}\varepsilon^0(k)-\varepsilon&V_1\\V_1&\varepsilon^0(k)-\varepsilon\end{matrix}\right|\Rightarrow \varepsilon=\varepsilon^0(k)\pm V_1$
• Dans le cas où $k=\pm p\frac{\pi}{a} ;\,p\in\mathbb N$, l’énergie est donnée par : $\varepsilon=\varepsilon^0(k)\pm V_p$
• Il en résulte que lorsque la bande croise un bord d’une zone de Brilloin, il y a apparition d’un bande interdite. Loin des bords, l’énergie est pratiquement identique à celle de l’électron libre.

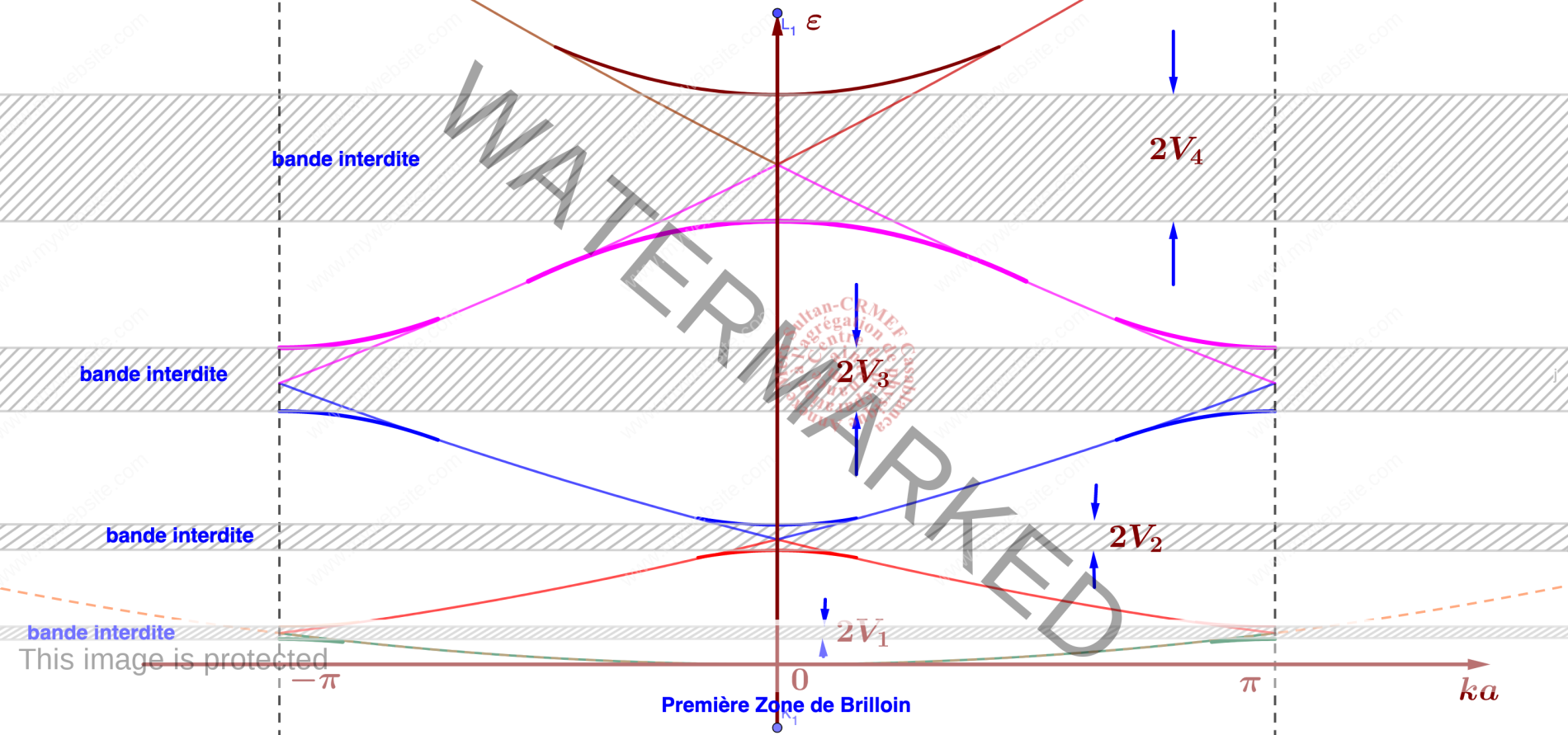
2.9. Approximation des liaisons fortes

• On considère une chaîne linéaire d’atomes équidistants de a et de longueur L=Na.
• Chaque atome apporte un électron à la bande étudiée. L’électron est localisé dans l’orbital $\phi$ lorsque l’atome est libre.
• On limite les interactions aux proches voisins. Il en résulte que les éléments de la matrice de l’hamiltonien monoélectronique sont donnés par : $\langle m|H_0|m\rangle=0 ;\,\langle m|H_0|m+1\rangle=-A ;\quad A>0$ où $\langle x|m\rangle=\phi_m(x)$.

• La résolution de l’équation de Schrödinger permet de déterminer l’énergie en fonction du nombre d’onde :  \begin{eqnarray*}\left\{\begin{gathered}\phi_k(x)=\sum_m\exp(ikma)\phi_m(x)\\ H_0|k\rangle=E|k\rangle\Rightarrow \sum_m\exp(ikma) H_0|m\rangle=E\sum_m\exp(ikma)|m\rangle\Downarrow \\ \sum_m\langle n|H_0|m\rangle\exp(ikma)=E\sum_m\exp(ikma)\delta_{mn}\end{gathered}\right.\Rightarrow E=-2A\cos(ka)\end{eqnarray*}
• on obtient une bande d’énergie. Chaque orbitale atomique donne lieu à une bande d’énergie. Les bandes d’énergie sont séparées par des bandes interdites.

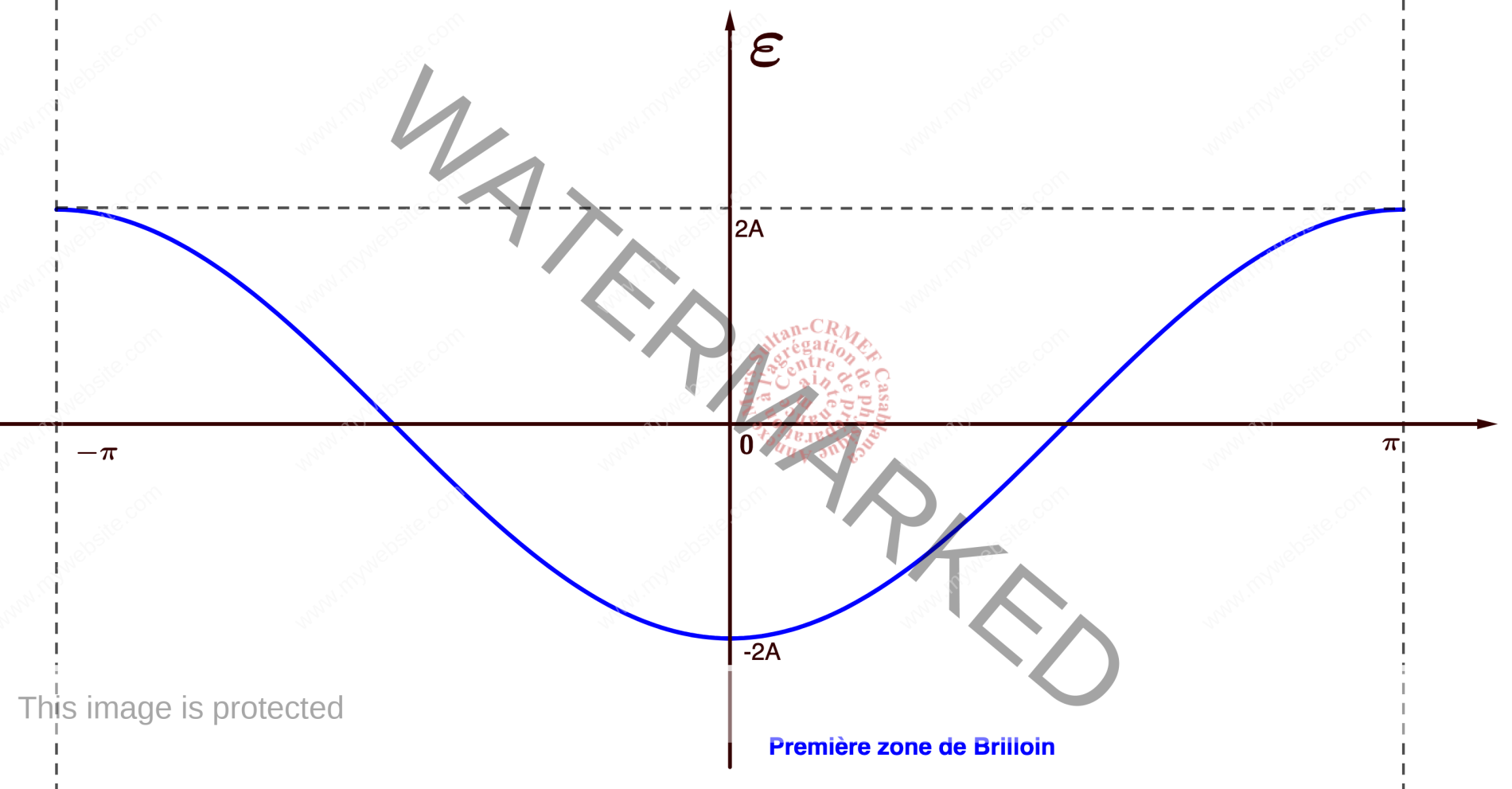
2.10. Cas général : bandes d’énergie du germanium

le sommet de la BV est situé au centre de la zone de Brillouin au point $\Gamma$. Ce maximum est constitué de la convergence de deux bandes qui sont dégénérées au sommet. Ces deux propriétés sont communes à tous les semiconducteurs à structure cubique. Compte tenu de l’unicité du point $\Gamma$ dans la première zone de Brillouin, le maximum de la bande de valence est unique. Le minimum de la bande de conduction est situé dans la direction (111) $\wedge$, à l’extrémité de la zone de Brillouin au point L. Il existe 8 directions $\wedge$ équivalentes, le gap est indirect.

2.11. Bandes d’énergie simplifiées

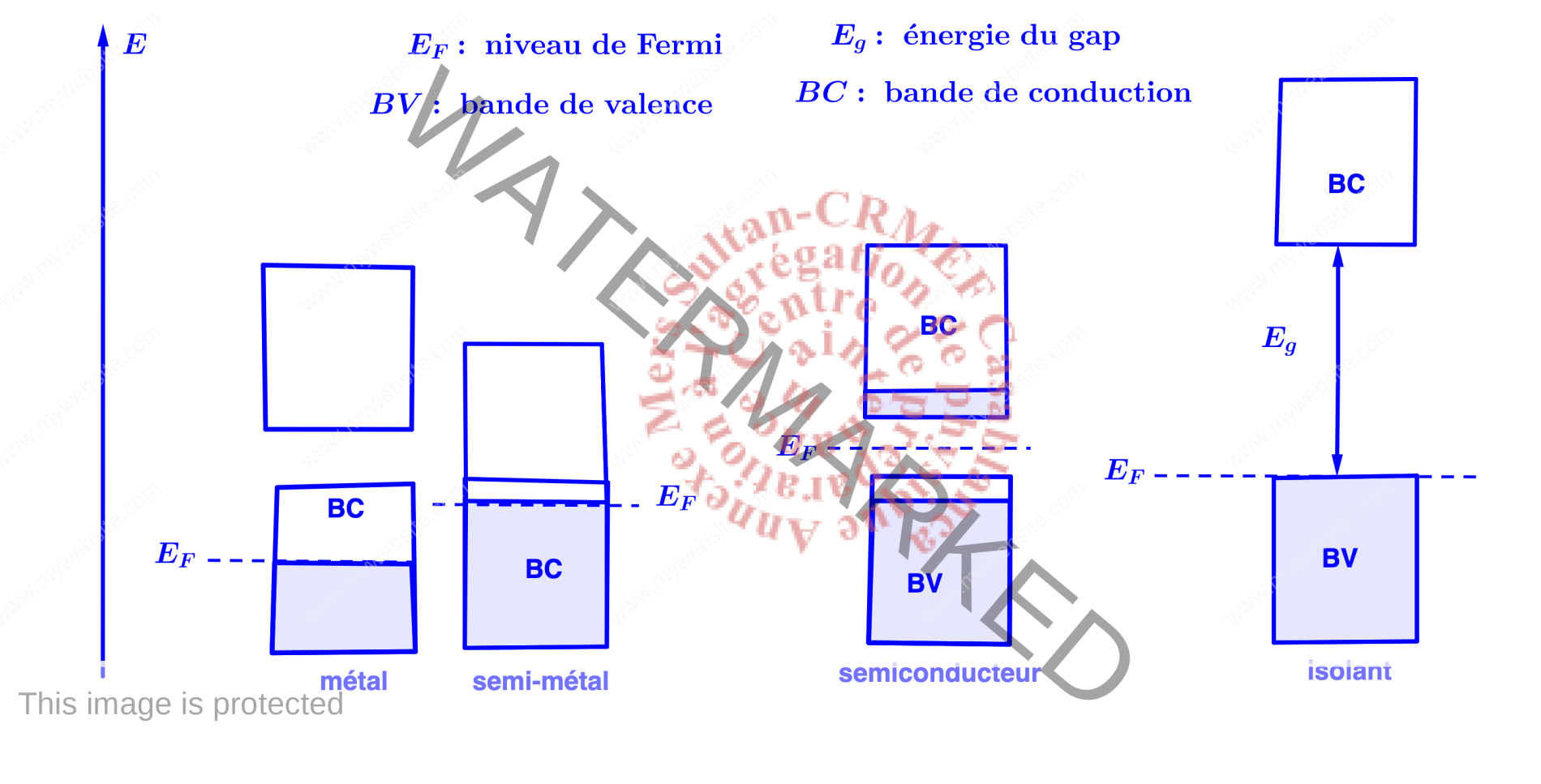
2.12. Qualification des matériaux Considérons le cas d’un cristal à N atomes tel que le volume de la maille élémentaire est $a^3$ : 

• N valeurs de $\overrightarrow k$ permises dans chaque bande et compte tenu du spin on a 2N états permis dans chaque bande.
• Dans le cas d’un cristal possédant un électron de valence par maille élémentaire, la bande de conduction est à moitié remplie : le cristal possède un caractère métallique. 
• Si le cristal possède un nombre paire d’électrons de valence et qu’il n’y a pas de chevauchement des bandes : le cristal a un comportement si l’énergie du gap est très grande devant $k_BT$.
• Lorsque l’énergie des états les plus élevés de la bande la plus basse est supérieure à celle des états les plus bas de la bande supérieure(chevauchement des deux bandes) le matériau possède un comportement métallique.
• Lorsque les deux dernières bandes occupées se chevauchent telles que le niveau de Fermi se situe dans un domaine de faible densité d’états, le matériau est qualifié de semi-métal.  
• Dans le cas où l’énergie du gap n’est pas très grande devant $k_BT$, le matériau est qualifié de semiconducteur.

2.13. Dynamique de l’électron dans le cristal : notion de masse effective La dynamique des électrons dans un semiconducteur fait intervenir la notion de masse effective :

• Au voisinage d’un extremum de bande situé en $\overrightarrow k_0$ dans le cas unidimensionnel peut  s’écrire sous la forme : $\varepsilon( k)=\varepsilon(k_0)+\frac{( k- k_0)^2}{2}\frac{d^2\varepsilon}{dk^2}(k_0)=\varepsilon\left(k_{0}\right)+\frac{\hbar^{2}\left(k-k_{0}\right)^{2}}{2 m^{\star}}$ $m^{\star}=\frac{\hbar^2}{\frac{d^{2} \varepsilon}{d k^{2}}\left(k_{0}\right)}$ est appelée masse effective de l’électron. Celle-ci peut être positive ou négative selon la concavité de l’énergie en fonction de k. 
• Cette expression se généralise au cas tridimensionnel par un tenseur dont les éléments sont donnés par : $\frac{1}{m_{i j}^{\star}}=\frac{1}{\hbar^{2}} \frac{\partial^{2} \varepsilon}{\partial k_{i} \partial k_{j}}$
• La vitesse de groupe pour une bande donnée s’exprime sous la forme : $\overrightarrow{v}_{\overrightarrow{k}}=\frac{1}{\hbar} \overrightarrow{\nabla}_{\overrightarrow{k}} \varepsilon(\overrightarrow{k})$. Il en résulte que la réponse à une force lentement variable dans le temps et dans l’espace s’exprime par : $\overrightarrow{F}=\hbar \frac{d \overrightarrow{k}}{d t}$

2.14. Dynamique de l’électron dans le cristal : notion de trou

• Considérons le cas de la bande de valence pleine. Dans ce cas $\sum_{tot}\overrightarrow k_e=\overrightarrow 0$.
• Le départ d’un électron $(\overrightarrow k_{e1})$ vers la bande de valance laisse une lacune appelée trou et caractérisé par $\overrightarrow k_t $ tel que :$\sum_{tot\text{ sauf }\overrightarrow k_{e1}}\overrightarrow k=-\overrightarrow k_{e1}=\overrightarrow k_t$. Le mouvement du trou est opposé à celui de l’électron dans la bande de valence. 
• Le trou possède une charge $+e$ opposée à celle de l’électron.
• l’énergie du trou est opposé à celle de l’électron dans la bande de valence : $\varepsilon_t(\overrightarrow k_t)=E_{tot,e}(T)-E_{tot,e}(0k)=-\varepsilon_e(\overrightarrow k_{e1})$ 
• Il en résulte que la masse effective du trou est opposée à celle de l’électron dans la bande de valence : $m^*_t=-m^*_e$
• les vitesses de groupe sont identiques. Exemple dans le cas de l’approximation parabolique : $\overrightarrow v_t=\frac{1}{\hbar}\nabla_{\overrightarrow k}\varepsilon_t=\frac{\hbar\overrightarrow k_t}{m^*_t}=\frac{1}{\hbar}\nabla_{\overrightarrow k}\varepsilon_e=\frac{\hbar\overrightarrow k_e}{m^*_e}=\overrightarrow v_e$ 

2.15. Semiconducteur intrinsèque : concentration des porteurs libres

• La distribution des électrons et des trous, à l’équilibre, est gouvernée par la statistique de Fermi-Dirac dont la probabilité d’occupation pour les électrons est donnée par : $f_{e}(\varepsilon)=\frac{1}{1+\exp\left(\frac{\varepsilon-\varepsilon_F}{kT}\right)}$
•   Celle des trous : $f_{t}(\varepsilon)=1-f_e(\varepsilon)=\frac{1}{1+\exp \left(\frac{\varepsilon_{F}-\varepsilon}{k T}\right)}$
• En tenant compte du fait que $|E-E_F|$ est supérieure à quelques $kT$, les distributions deviennent celles de Boltzmann : $f_e(\varepsilon)\approx \exp\left(-\frac{\varepsilon-\varepsilon_F}{kT}\right) ;\quad f_t(\varepsilon)\approx \exp\left(-\frac{\varepsilon_F-\varepsilon}{kT}\right)$

• La concentration des électrons dans la bande de conduction s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}n=\int_{\varepsilon_C}^{\varepsilon_{max}}n_c(\varepsilon)f_e(\varepsilon)d\varepsilon\approx \int_{\varepsilon_C}^\infty n_c(\varepsilon)f_e(\varepsilon)d\varepsilon\\ \underbrace{n_C(\varepsilon)=\frac{1}{2\pi^2}\left(\frac{2m^*_e}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{\varepsilon-\varepsilon_C}}_{\text{densite d’etats dans la bande de conduction}}\Downarrow \\ n=N_C\exp\left(-\frac{\varepsilon_C-\varepsilon_F}{kT}\right) ;\quad \underbrace{N_C=2\left(\frac{2\pi m^*_ekT}{h^2}\right)^{3/2}}_{\text{densite equivalente d’etats rammenee en }\varepsilon_C}\end{gathered}\right.\end{eqnarray*}

• La concentration des trous dans la bande de valence s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}p=\int_{\varepsilon_{min}}^{\varepsilon_V}n_V(\varepsilon)f_t(\varepsilon)d\varepsilon\approx \int_{-\infty}^{\varepsilon_V} n_V(\varepsilon)f_t(\varepsilon)d\varepsilon\\ \underbrace{n_V(\varepsilon)=\frac{1}{2\pi^2}\left(\frac{2m^*_t}{\hbar^2}\right)^{\frac{3}{2}}\sqrt{\varepsilon_V-\varepsilon}}_{\text{densite d’etats dans la bande de valence}}\Downarrow \\ p=N_V\exp\left(-\frac{\varepsilon_F-\varepsilon_V}{kT}\right) ;\quad \underbrace{N_V=2\left(\frac{2\pi m^*_tkT}{h^2}\right)^{3/2}}_{\text{densite equivalente d’etats rammenee en }\varepsilon_V}\end{gathered}\right.\end{eqnarray*}

• Loi d’action de masse : $np=N_CN_V\exp\left(-\frac{E_g}{kT}\right)$. Le produit ne dépend que de la température et de l’énergie du gap.
• Un semiconducteur intrinsèque est caractérisé par $n_i=p_i=\sqrt{N_CN_V}\exp\left(-\frac{E_g}{2k_BT}\right)$
• Il en résulte le niveau de Fermi pour le semiconducteur intrinsèque : $\varepsilon_{Fi}=\frac{\varepsilon_V+\varepsilon_C}{2}-\frac{kT}{2}\ln\left(\frac{N_C}{N_V}\right)$
• La conductivité électrique du semiconducteur intrinsèque s’obtient de la manière suivante : $\overrightarrow J=e(n\mu_n+p\mu_p)\overrightarrow E\Rightarrow \sigma=e(n_i\mu_e+p_i\mu_p)=e(\mu_n+\mu_p)\sqrt{N_CN_V}\exp\left(-\frac{E_g}{2k_BT}\right)$
• La résistivité électrique est l’inverse de la conductivité $\rho=\sigma^{-1}=\frac{1}{e(\mu_n+\mu_p)\sqrt{N_CN_V}}\exp\left(\frac{E_g}{2k_BT}\right)=a\exp\left(\frac{b}{T}\right) ;\quad a=cste ;\,b=\frac{E_g}{2k_B}$