Résistivité électrique du germanium dopé P Effet Hall classique dans Ge(P)
Évolution de la résistivité électrique en fonction de la température
Évolution du coefficient de Hall en fonction de la température
Évolution de la mobilité des porteurs de charge en fonction de la température.
Montage expérimental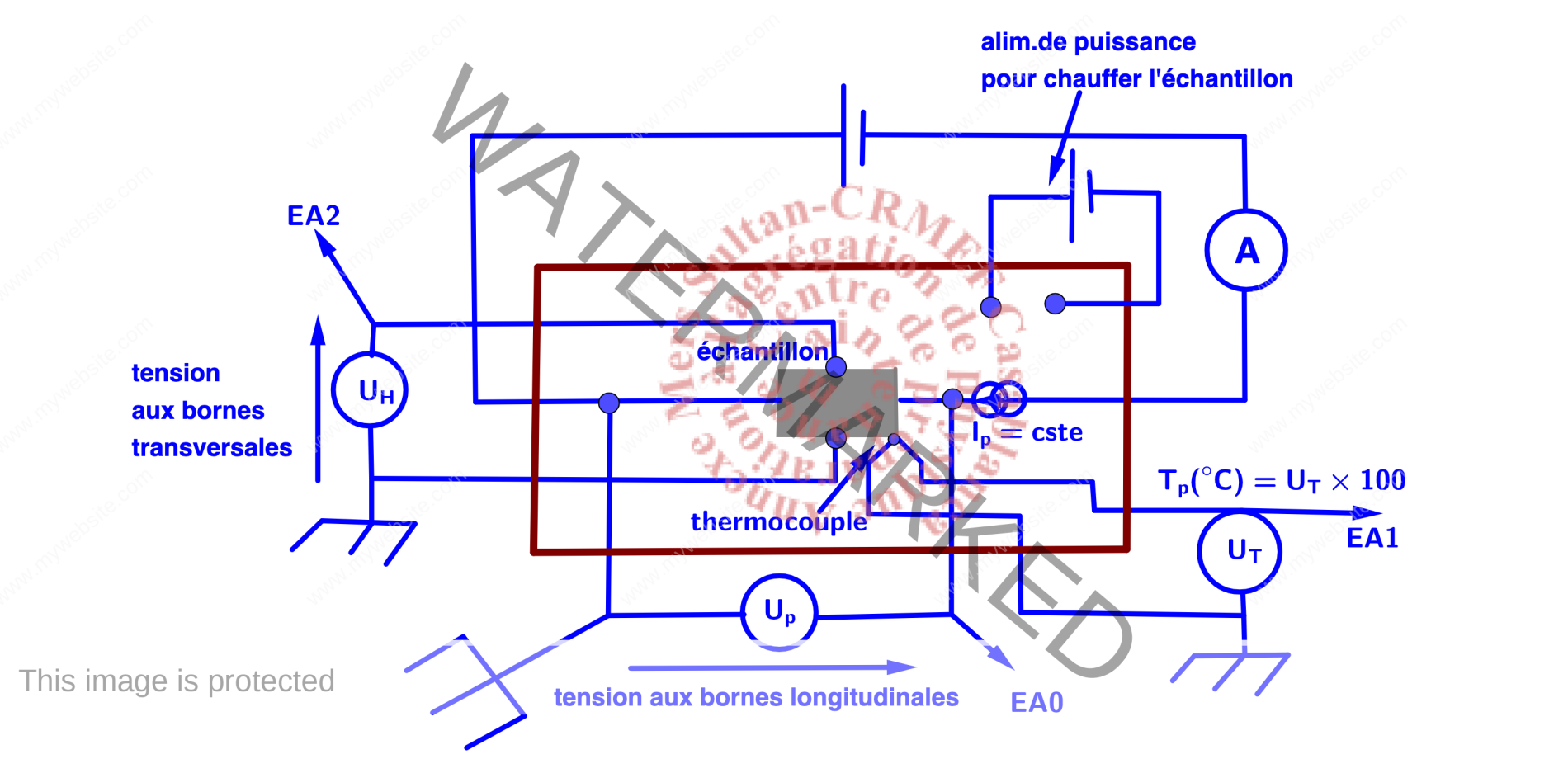
- Console à effet Hall avec son alimentation(transformateur-redresseur)
- Alimentation stabilisée de puissance,
- platine avec cristal de germanium non dopé,
- capteur de champ magnétique à effet Hall,
- bobines avec noyau en U,
- multimètres,
- Carte d’acquisition+PC
- fils électriques.
1. Définition d’un semi-conducteur dopé P
Un semiconducteur est un matériau caractérisé par une résistivité électrique $\rho$ très inférieure à celle des isolants et très grande par rapport à celle des conducteurs :
$10^{-5}\,\Omega.cm^{-1}\ll \rho \ll 10^{8}\,\Omega.cm^{-1}$. Une plage de $\rho(\Omega.cm^{-1})$ peut être : $\rho \in[10^{-3}, 10^{4}]$.
En réalité seule une étude dans le cadre de la mécanique quantique, tenant compte du caractère cristallin du matériau, apporte une réponse claire à la question. Pour plus de précisions voir la vidéo sur la résistivité électrique du germanium intrinsèque. « Conductivité électrique d’un semi-conducteur intrinsèque »
Un semiconducteur est dopé P est un semiconducteur auquel on a ajouté une quantité très faible d’impuretés ayant 3 électrons de valence. Les impuretés qui peuvent être ajoutés sont l’indium, le bore, le gallium,$\ldots$ L’impureté ajoutée établit des liaisons covalentes avec les atomes de germanium. Il se créé un état vacant appelé trou et une charge négative fixe sur l’impureté. Ces trous chargés positivement peuvent se déplacer d’un atome à l’autre dans le matériaux semi-conducteur lorsque les électrons quittent leur position. Cette opération se traduit en terme de bandes d’énergie par un niveau d’énergie accepteur d’électrons proche du bas de la bande de valence comme le montre le schéma suivant.
Le dopage se manifeste dans les bandes d’énergie du semiconducteur par l’apparition d’un niveau accepteur juste au dessus du maximum de la bande de valence d’énergie $E_a$. La différence d’énergie $E_a-E_V$ est faible, des électrons de la bande de valence sont excités thermiquement et peuplent ce niveau. Ils laissent derrière eux des trous dans la bande de valence. On peut dire que la densité des trous créés par ce processus est pratiquement égale à la densité des impuretés acceptrices $N_a$.
2. Résistivité électrique d’un semiconducteur 2.1. Domaine proche de la température ambiante Dans ce domaine les dopants sont complètement ionisés. La densité électronique dans la bande de conduction est $n=N_d$ ou $N_d$ est le nombre de dopants par unité de volume. La conductivité électrique et par suite la résistivité s’expriment sous la forme : $\sigma=en\mu_n\Rightarrow \rho=\frac{1}{e\mu_n N_d}$ L’évolution en fonction de la température de la résistivité électrique est due à l’évolution de la mobilité électrique des électrons en fonction de la température. Les mécanismes qui gouvernent cette loi sont la diffusion par les impuretés et par le réseau cristallin.
2.2. Domaine des hautes températures À haute température le régime intrinsèque domine, c’est à dire la densité des électrons dans la bande de conduction et celle des trous dans la bande de valence sont dues à sont l’excitation thermique : $n=n_i=p=\sqrt{N_CN_V}\exp\left(-\frac{E_g}{2k_BT}\right)$ Il en résulte que la résistivité du matériau devient sous la forme : $\rho=\frac{1}{en_i(\mu_n+\mu_p)}=a\exp\left(\frac{b}{T}\right) ;\,a=\frac{1}{e\sqrt{N_cN_V}(\mu_n+\mu_p)} ;\quad b=\frac{E_g}{2k_B}$ où $\mu_n$ et $\mu_p$ désignent respectivement les mobilité des électrons et des trous, $N_C$ la densité équivalente d’états ramenée en $\varepsilon_C$, $N_V$ celle ramenée en $\varepsilon_V$ et $E_g$ représente le gap du semiconducteur.
3. Effet Hall classique dans un semiconducteur dopé N
3.1. Définition de l’effet Hall
C’est l’apparition d’une tension électrique entre les faces latérales d’un barreau conducteur ou semiconducteur traversé par un courant électrique et placé dans un champ magnétique perpendiculaire à la direction du passage du courant. Le signe de la tension de Hall dépend de la nature des porteurs de charge majoritaires. Elle est positive pour un conducteur métallique et un semiconducteur de type N et elle est négative pour un semiconducteur de type P comme le montre les figures suivantes.
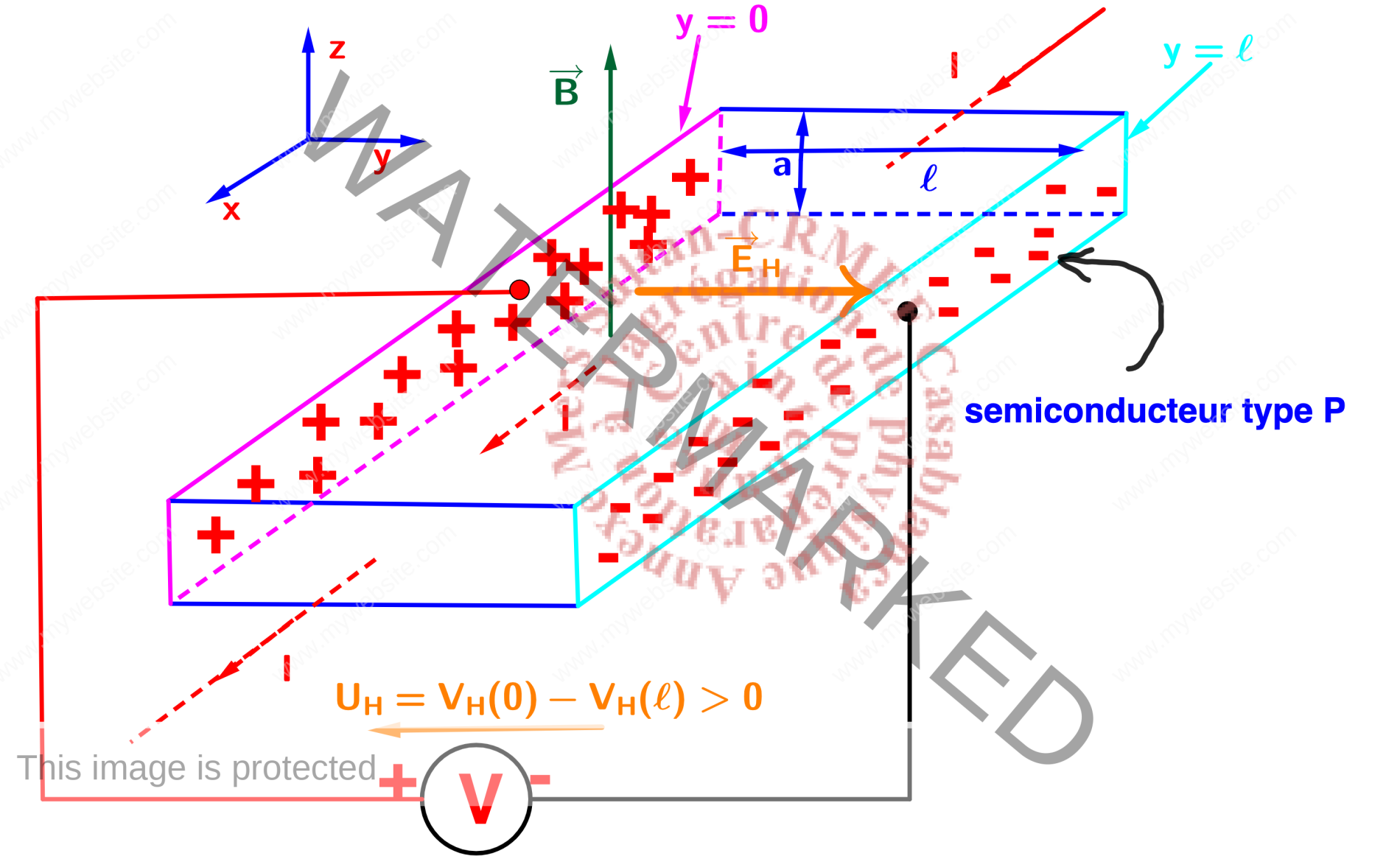
3.2. Expression de la tension de Hall On utilise un modèle simplifié qui repose sur les hypothèses ci-dessous
- On suppose que tous les porteurs de charge d’un même type ont la même vitesse de dérive(valeur moyenne)
- on ne tient pas compte des collisions avec les atomes du cristal
- on se place en régime permanent
- le courant électrique est suivant l’axe Ox : $\overrightarrow J=\frac{I}{S}\overrightarrow e_x ;\,S=a\ell\overrightarrow e_x$
- Le paramètre $R_H=\frac{-1}{ne}$ est appelée coefficient de Hall.
- La tension de Hall s’exprime en fonction du coefficient de Hall selon la définition par : $U_H=\pm R_H\frac{IB}{a}$
- Connaissant la conductivité électrique on peut déterminer la mobilité des électrons : $\sigma=en\mu_n\Rightarrow \mu_n=-R_H\sigma$
- Le paramètre $R_H=\frac{1}{pe}$ est appelée coefficient de Hall.
- La tension de Hall s’exprime en fonction du coefficient de Hall selon la définition par : $U_H=\pm R_H\frac{IB}{a}$
- Connaissant la conductivité électrique on peut déterminer la mobilité des électrons : $\sigma=ep\mu_p\Rightarrow \mu_p=R_H\sigma$
En fait certains porteurs sont plus rapides, d’autres plus lents. Le champ de Hall, qui est un effet moyen, n’équilibre donc pas la force de Lorentz pour tous les porteurs. Les plus rapides sont déviés dans un sens par la force de Lorentz qui pour eux n’est pas entièrement compensée par la force de Hall, les plus lents sont déviés dans l’autre sens par la force de Hall qui pour eux est supérieure à la force de Lorentz. Ainsi en présence du champ magnétique les trajectoires des porteurs ne sont pas toutes longitudinales, il existe des courants transversaux dont la somme algébrique est nulle puisque le courant total suivant $y$ reste nul en raison de l’absence de connexion latérale. Les porteurs dont la trajectoire est déviée latéralement ont une composante longitudinale de vitesse qui de ce fait diminue, il en résulte une diminution du courant longitudinal c’est-à-dire de la conductivité du matériau, cet effet porte le nom de magnétorésistance transversale. Le traitement rigoureux
se fait à l’aide de l’équation de transport de Boltzmann
