• Obtenir l’évolution de la tension aux bornes du condensateur en fonction du temps, lorsqu’on ferme le circuit constitué d’un générateur de tension alternative, d’une résistance de résistance R et d’un condensateur de capacité C.
• Ajuster la courbe expérimentale $u_c(t)$ au modèle donné par : \begin{eqnarray*}u_c=\frac{E}{1+\omega^2\tau^2}\left[\cos(\omega t)-\exp\left(-\frac{t}{\tau}\right)\right]+\frac{E\omega\tau}{1+\omega^2\tau^2}\sin(\omega t)\end{eqnarray*}
• Comparer la valeur de la constante de temps $\tau$ à celle calculée à partir des valeurs de données par le constructeur.

Montage expérimental

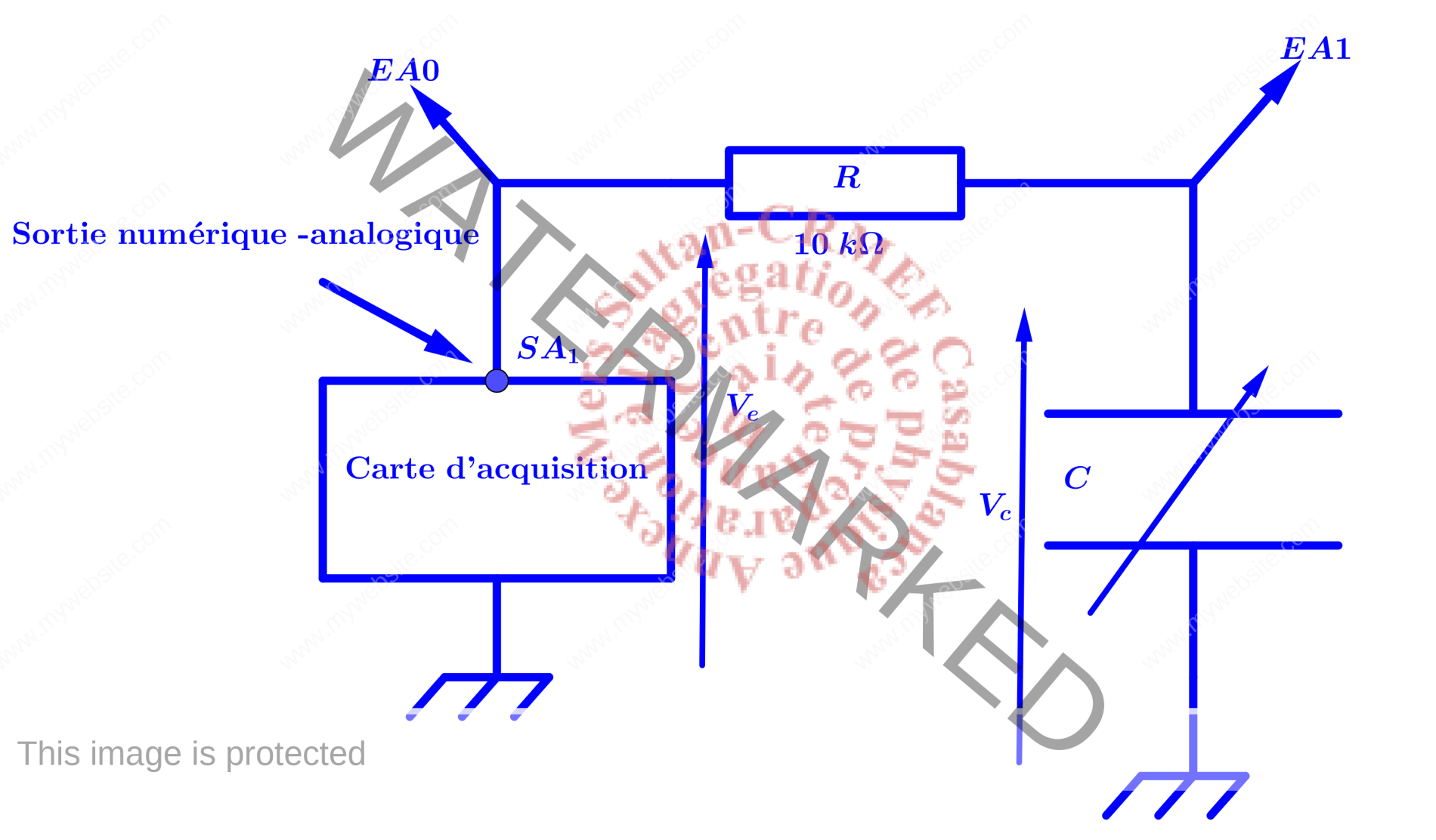
• Carte d’acquisition+PC, 
• oscilloscope numérique,
• boite à décades de résistances,
• boite à décades de capacités,
• fils électriques.

\begin{eqnarray*}\Large u_e=E\cos(\omega t)=Ri+u_c ;\quad i=C\frac{du_c}{dt} ;\quad\tau=RC\Downarrow\\\Large\frac{du_c}{dt}+\frac{u_c}{\tau}=\frac{E\cos(\omega t)}{\tau}\Downarrow \\ \Large u_c=\alpha\exp\left(-\frac{t}{\tau}\right)+\frac{E}{1+\omega^2\tau^2}\cos(\omega t)+\frac{E\omega\tau}{1+\omega^2\tau^2}\sin(\omega t)\\ \Large u_c(0)=0\Downarrow \\\Large u_c=\frac{E}{1+\omega^2\tau^2}\left[\cos(\omega t)-\exp\left(-\frac{t}{\tau}\right)\right]+\frac{E\omega\tau}{1+\omega^2\tau^2}\sin(\omega t)\end{eqnarray*}