- Mise en évidence expérimentale de l’effet Peltier
- étude de la pompe à chaleur Peltier
- détermination de coefficient Seebeck, de la conductivité thermique du module Peltier et du coefficient d’échange thermique avec l’extérieur
Montage expérimental : module Peltier
Montage expérimental : Mise en évidence expérimentale de l’effet Peltier
Pompe à chaleur Peltier
Montage expérimental : phase pompe à chaleur
Montage expérimental : phase de refroidissement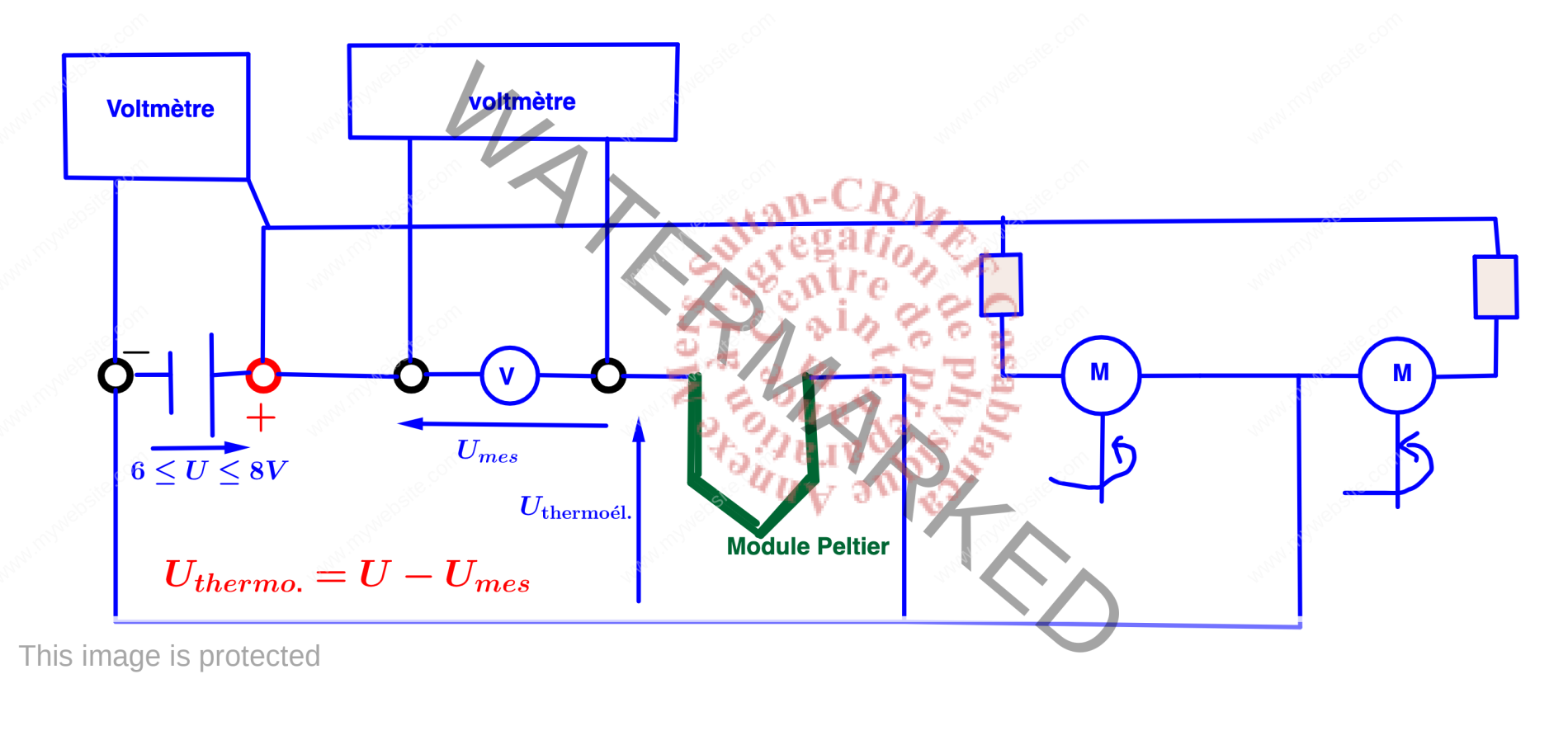
- Module Peltier,
- pompe à chaleur Peltier,
- sondes de température,
- multimètres numériques,
- carte d’acquisition+PC
1. Mise en évidence expérimentale de l’effet Peltier
1.1. Définition de l’effet Peltier
L’effet Peltier est l’effet thermique autre que l’effet Joule qui se passe au niveau d’une jonction de deux matériaux de nature différente traversée par un courant électrique : suivant le sens du courant de la chaleur (transfert thermique) est absorbée ou générée. L’effet Peltier est l’effet réciproque de l’effet Seebeck. La mise en équation passe par l’utilisation de la théorie de la réponse linéaire d’Onsager. C’est une théorie macroscopique du couplage linéaire des phénomènes irréversibles(électrique et thermique par exemple). Ci-après quelques notions succinctes.1.2. Couplage thermoélectrique
1.2.1. Schéma synoptique
- Les coefficients phénoménologiques $L_{ii}$ sont reliés aux conductivités électrique $\gamma$ et thermique $\lambda$
- les coefficients phénoménologiques $L_{ij\neq i}$ traduisent le couplage thermoélectrique. En absence d’interaction magnétique et de force de Coriolis, ils vérifient les relations de réciprocité d’Onsager : $L_{ik}=L_{ki}$. L’influence de la force thermodynamique $\overrightarrow F_i$sur le courant volumique $\overrightarrow j_k$ est égal à celui qui traduit l’influence de la force $\overrightarrow F_k$ sur le courant volumique $\overrightarrow J_i$
- en présence d’un champ magnétique et/ou le système thermodynamique est en rotation à la vitesse $\overrightarrow \Omega$, les relations d’Onsager deviennent : $$L_{ik}(\overrightarrow B,\overrightarrow \Omega)=L_{ki}(-\overrightarrow B,-\overrightarrow \Omega)$$
- Conduction électrique seule (température uniforme $\overrightarrow F_{th}=\overrightarrow 0$) : $$\overrightarrow J_e=-\gamma\overrightarrow{\rm grad}V=-\frac{L_{ee}}{T}\overrightarrow{\rm grad}V\Rightarrow \gamma=\frac{L_{ee}}{T}$$
- conduction thermique en absence de phénomène électrique $(\overrightarrow F_e=\overrightarrow 0)$ : $$\overrightarrow J_{th}=-\lambda\overrightarrow{\rm grad}T=-\frac{L_{tt}}{T^2}\overrightarrow{\rm grad}T\Rightarrow \lambda=\frac{L_{tt}}{T^2}$$
- Effet Seebeck(conduction thermique en circuit ouvert $\overrightarrow J_e=\overrightarrow 0$) : $$\overrightarrow J_e=\overrightarrow 0\Rightarrow \overrightarrow{\rm grad}V=-\varepsilon \overrightarrow{\rm grad}T$$ $\varepsilon$ est appelé coefficient Seebeck. Il s’exprime sous la forme : $$\varepsilon=\frac{L_{et}-L_{ee}V}{TL_{ee}}\Rightarrow \lambda=\frac{L_{tt}-L_{te}(V+\varepsilon T)}{T^2}=\frac{L_{ee}L_{tt}-L_{te}^2}{T^2L_{ee}}$$

1.2.5. Courants thermoélectriques
- Vecteur densité de courant électrique : $$\overrightarrow J_e=\gamma T(\varepsilon T+V)\overrightarrow{\rm grad}\left(\frac{1}{T}\right)-\gamma T\overrightarrow{\rm grad}\left(\frac{V}{T}\right)$$
- Vecteur densité de courant d’énergie thermique : $$\overrightarrow J_{th}=-\lambda\overrightarrow{\rm grad}T+(\varepsilon T+V)\overrightarrow J_e$$
- Cas particulier (température uniforme $\overrightarrow{\rm grad}T=\overrightarrow 0$) : $$\overrightarrow J_e=-\gamma \overrightarrow{\rm grad}V ;\quad \overrightarrow J_{th}=(\varepsilon T+V)\overrightarrow J_e$$
- L’effet Peltier est l’effet thermique, autre que l’effet Joule, qui accompagne le passage d’un courant à travers une jonction entre de matériaux différents à la même température T. Le vecteur densité volumique de courant thermique dû à l’effet Peltier s’exprime par : $$\overrightarrow J_{thP}=\varepsilon T\overrightarrow J_e$$
- Dans le cas d’une jonction entre deux matériaux A et B, la puissance reçue par celle-ci s’obtient de la manière suivante : $$P_{recuePeltier}=\underbrace{\iint \overrightarrow J_{th,P}\overrightarrow n_{int} dS}_{\text{integrale double fermee}}=T(\varepsilon_A-\varepsilon_B)I_{A\longrightarrow B}$$

On augmente la puissance fournie à la source froide en mettant N unités Sc(n)-Sc(p) en série : $$P_{\text{fournie a la source froide}}=NT_F(\varepsilon_n-\varepsilon_p)I=-ST_FI$$ où S est appelé le coefficient Seebeck du module Peltier.
Le matériau utilisé dans le module Peltier est le tellure de bismuth qui possède les propriétés suivantes :
- une conductivité électrique élevée,
- un coefficient Seebeck important
- une faible conductivité thermique.
Expérience en vidéo
Mise en évidence de l’effet Peltier
Expérience en vidéo
Mise en évidence de l’effet Peltier
[download id="8092"]
Expérience en vidéo
Pompe à chaleur Peltier
Expérience en vidéo
Pompe à chaleur Peltier
