Oscillateur de Van der Pol
- Étude des éléments constitutifs de l’oscillateur de Van der pol,
- comprendre l’entretien des oscillations d’un oscillateur électrique
Montage expérimental (circuit non linéaire)
Montage expérimental(oscillateur harmonique)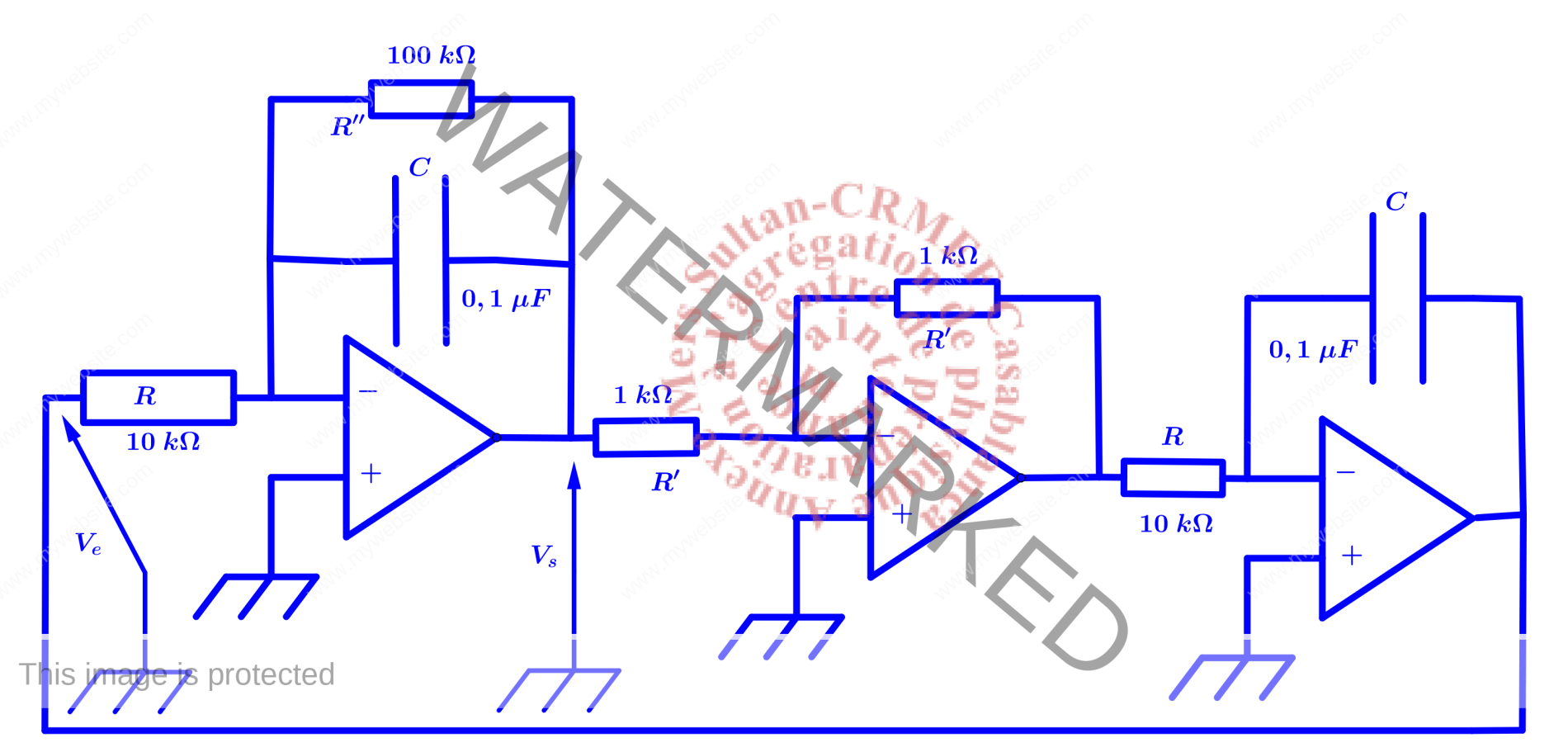
Montage expérimental(oscillateur de Van der pol)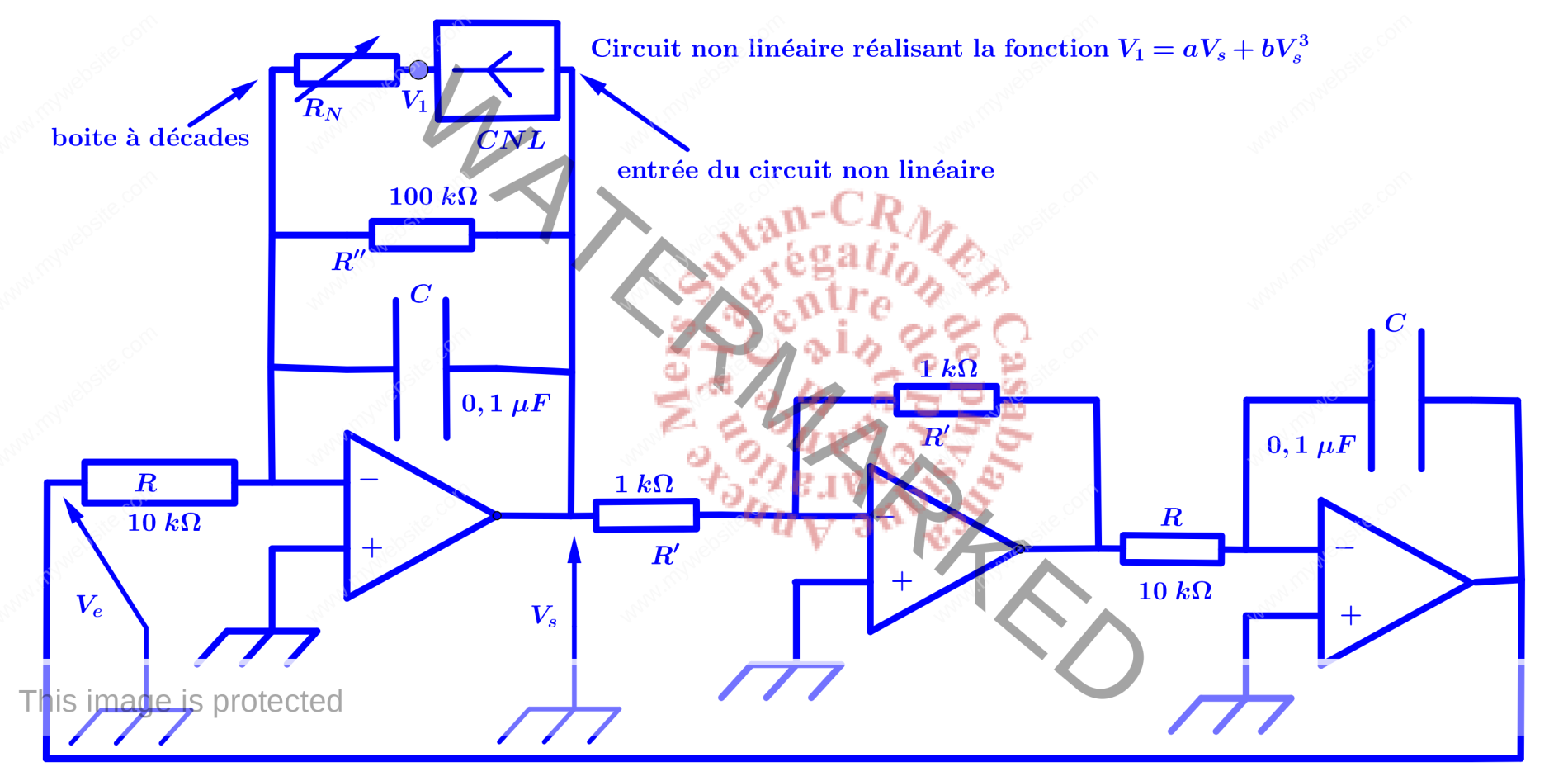
Montage expérimental(régime permanent et conditions initiales)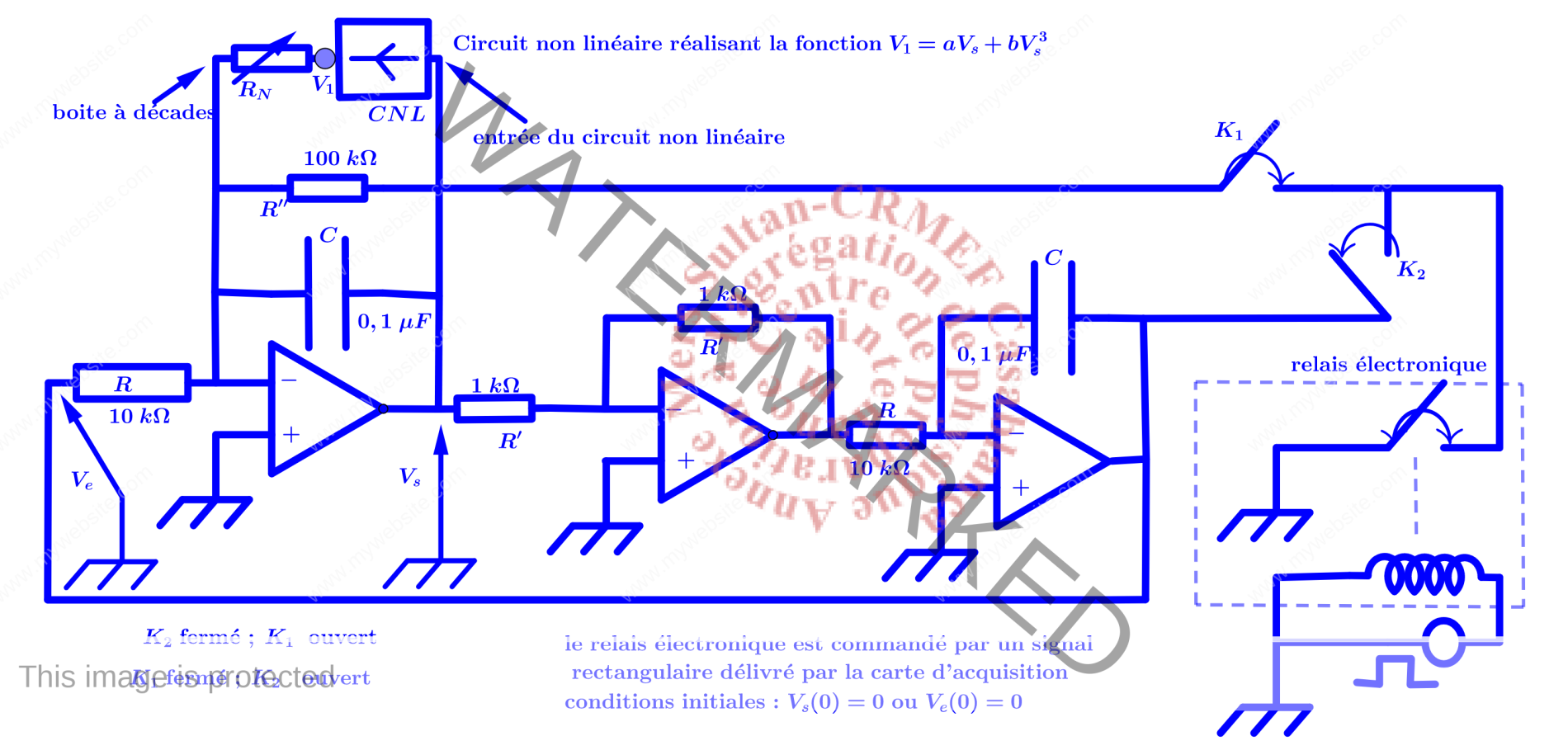
- Oscilloscope,
- GBF,
- multimètres,
- résistances, $1\,k\Omega$, $10\,k\Omega$, $2,25\,k\Omega$,$5\,k\Omega$, $75\,k\Omega$ $100\,k\Omega$,
- multiplieurs AD633, ampli. TL081,
- condensateurs, $c=0,1\,\mu F$
- Carte d’acquisition+PC
- relais électronique
- Fils électriques
1.1. Pourquoi étudier l’oscillateur de Van Der Pol ? car il constitue un modèle approché d’un grand nombre d’oscillateurs réels et permet d’expliquer l’entretien des oscillations . Il permet en plus de visualiser l’évolution du régime quasisinusoïdal des oscillations vers le régime de relaxation moyennant la variation d’un paramètre.1.2. Quelles sont les caractéristiques d’un oscillateur harmonique ?
- la linéarité : il y a invariance de l’équation $\ddot x+\omega_0^2x=0$ par dilatation, c’est à dire lorsqu’on change x par $\lambda x$ où $\lambda$ est réel.
- la réversibilité : il y a invariance de l’équation différentielle par renversement du temps . Ceci est dû au fait qu’il n’y a pas de phénomènes dissipatifs.
En conclusion, le modèle recherché fait appel à un oscillateur harmonique amorti et à un circuit non linéaire. L’équation de van der pol s’exprime par : \begin{eqnarray*}\ddot x-\varepsilon \omega_0\left(1-\frac{x^2}{x_0^2}\right)\dot x+\omega_0^2x=0\end{eqnarray*}La réalisation expérimentale s’effectue de proche en proche. On commence par le schéma de l’oscillateur harmonique donné dans la figure ci-dessous.
En suite, le dipôle non linéaire en série avec une résistance $R_N$ donné ci-dessous.
La combinaison de ces deux circuits conduit au schéma du montage de l’oscillateur de van der pol donné comme suit :
2. Réalisation de la fonction $V_s=aV_a+bV_e^3$ à l’aide d’un circuit non linéaire
Le montage est donné dans la figure ci-dessous.
On suppose que l’amplificateur opérationnel est idéal et fonctionne en régime linéaire. La tension de sortie $V_s$ s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}V^+=V^-=\frac{R_4}{R_4+R_3}\\\frac{KV_e^2-V^-}{R_1}+\frac{V_{sampli}-V^-}{R_2}=0\\V_s=KV_eV_{sampli}\end{gathered}\right.\Rightarrow\left\{\begin{gathered}V_s=\frac{R_2}{R_1}KV_e^3-K\frac{R_4}{R_4+R_3}\frac{R_1+R_2}{R_1}V_0V_e=aV_e+bV_e^3\Downarrow\\a=-K\frac{R_4}{R_4+R_3}\frac{R_1+R_2}{R_1}V_0 ;\quad b=\frac{R_2}{R_1}K\end{gathered}\right.\end{eqnarray*}
3. Oscillateur de van der pol On suppose que les amplificateurs opérationels sont idéaux et fonctionnent en régime linéaire. L’équation différentielle de l’oscillateur s’obtient de la manière suivante : \begin{eqnarray*}\left\{\begin{gathered}\underbrace{\frac{V_e-V^-}{R}+C\frac{d(V_s-V^-)}{dt}+\frac{V_s-V^-}{R”}+\frac{aV_s+bV_s^3}{R_N}=0}_{\text{loi des noeuds au niveau de la borne inverseuse du premier ampli.}}\\\text{le deuxieme ampli. est un montage inverseur il transforme Vs en -Vs}\\ \underbrace{\frac{-V_s-V^-}{R}+C\frac{d(V_e-V^-)}{dt}=0}_{\text{loi des noeuds au niveau de la borne inverseuse du troisieme ampli.}}\ ;\quad V^-=V^+=0\\V_1=aV_s+bV_s^3\end{gathered}\right.\Rightarrow \left\{\begin{gathered}\frac{d^2V_s}{dt^2}+\frac{R_N+aR”}{CR”R_N}\left(1+\frac{3bR”}{R_N+aR”}V_s^2\right)\frac{dV_S}{dt}+\frac{V_s}{R^2C^2}=0\Downarrow\\\frac{d^2V_s}{dt^2}-\varepsilon\omega_0\left(1-\frac{V_s^2}{S_0^2}\right)\frac{dV_S}{dt}+\omega_0^2V_s=0\Downarrow\\S_0^2=-\frac{R_N+aR”}{3bR”} ;\quad\omega_0^2=\frac{1}{R^2C^2} ;\quad\varepsilon=-\frac{R(aR”+R_N)}{R_NR”}\end{gathered}\right.\end{eqnarray*}La naissance de oscillations exige que $\varepsilon\geq 0$, c’est à dire $R_N\leq-aR”$. Lorsque $R_N $ est légèrement inférieur à $-aR”$, les oscillations sont quasi-sinusoïdales d’amplitude $V_{sm}=2S_0\Rightarrow V_{sm}^2=-\frac{4}{3bR”}(R_N+aR”)$. $V_{sm}^2=f(R_N)$ est une droite de pente $-\frac{4}{3bR”}$ et d’ordonné à l’origine $-\frac{4a}{3b}$. Ce qui pêrmet de déterminer a et b.
4. Régime permanent et conditions initiales
Le montage est donné dans la figure ci-dessous.
