• Visualiser la caractéristique courant-tension d’un dipôle à résistance négative
• Étudier les phases d’amorçage et d’amortissement des oscillations d’un oscillateur rLC à résistance négative
• Entretenir les oscillations d’un oscillateur rLC à résistance négative

Montage expérimental : caractéristique courant-tension d’un dipôle à résistance négative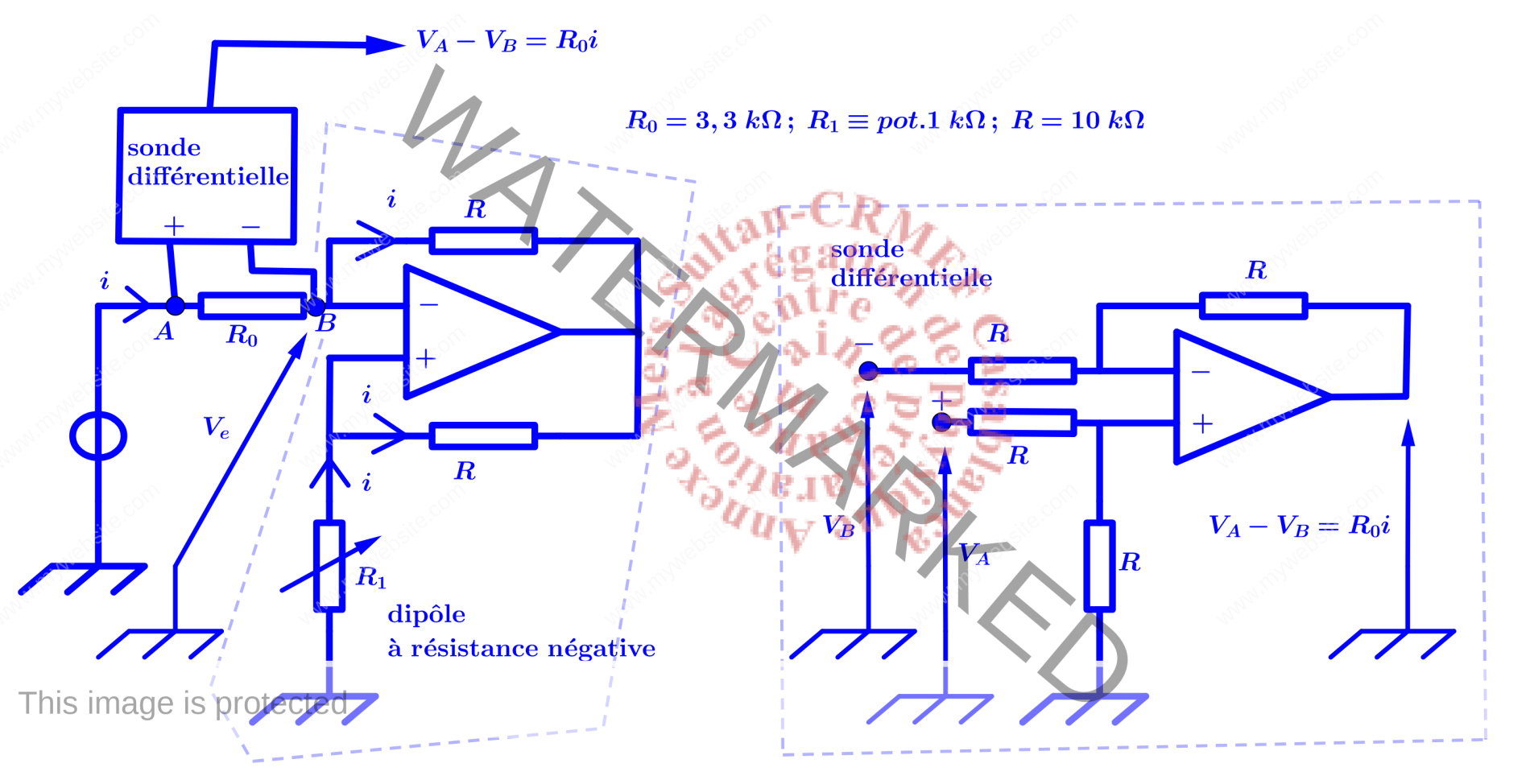

Montage expérimental : phases d’amorçage et d’amortissement des oscillations d’un oscillateur rLC à résistance négative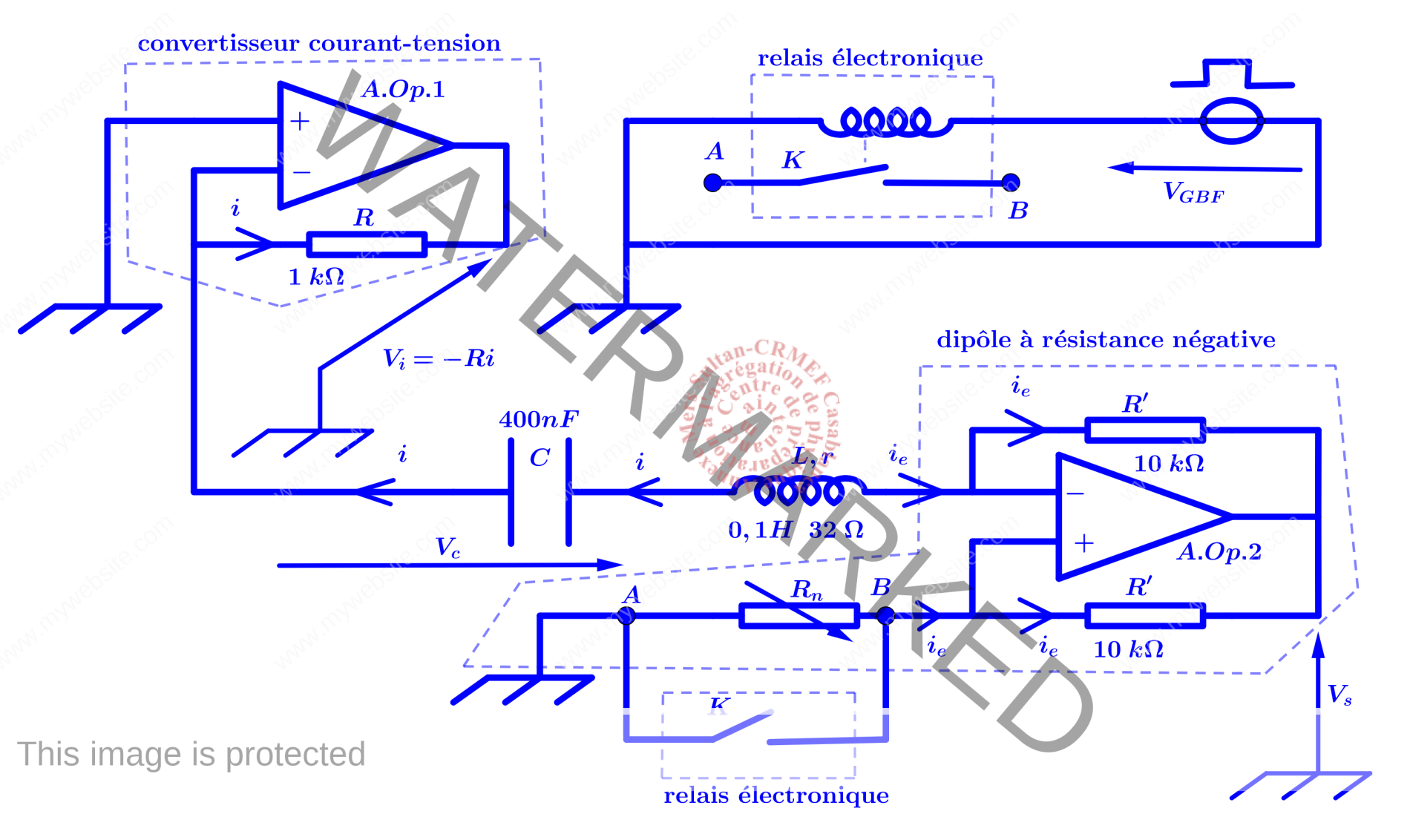

Montage expérimental : entretien des oscillations d’un oscillateur rLC à résistance négative

• Carte d’acquisition+PC,
• Oscilloscopes,
• Boite à décades de résistances,
• Boite à décades de capacités,
• GBF,
• Ampli. TL081,
• Résistances et capacités,
• Relais électronique,
• Fils électriques.

1. Dipôle à résistance négative Le montage synoptique est donné dans la figure ci-dessous.Les régimes de fonctionnement du montage sont donnés ci-desssous :

\begin{eqnarray*}\left\{\begin{gathered}\underbrace{\varepsilon=V^+-V^-=0,\quad V_e=-R_1i=\frac{R_1}{R_1+R}V_s ;\quad |V_s|<V_{sat}\Rightarrow |V_e|<\frac{R_1}{R_1+R}V_{sat}=V_b ;\quad |i|<\frac{V_b}{R_1}}_{\text{regime lineaire}}\\ \underbrace{\varepsilon>0 ;\quad V_s=+V_{sat}\Rightarrow V_e=V_{sat}+Ri ;\quad V^+=V_b ;\quad V_e=V^-<V_b\Rightarrow i<-\frac{V_b}{R_1}}_{\text{Ampli Op. en regime de saturation haute}}\\\underbrace{\varepsilon<0 ;\quad V_s=-V_{sat}\Rightarrow V_e=-V_{sat}+Ri ;\quad V^+=-V_b ;\quad V_e=V^->-V_b\Rightarrow i>\frac{V_b}{R_1}}_{\text{Ampli Op. en regime de saturation basse}}\end{gathered}\right.\end{eqnarray*}Le graphe ci-dessous montre les différents régimes de fonctionnement du montage.

2. Oscillateur à résistance négative

2.1. Phases d’amorçage et d’amortissement des oscillations d’un oscillateur à résistance négative Le schéma du montage expérimental est donné dans la figure ci-dessous.

L’amplificateur opérationnel A.Op.1 fonctionne en régime linéaire. On suppose que l’A.Op.2 fonctionne en régime linéaire. On peut remplacer le montage du dipôle à résistance négative par une résistance dynamique $-R_n$ comme le montre le schéma synoptique ci-dessous.

• Lorsque l’interrupteur K est ouvert l’équation différentielle du circuit s’obtient comme suit : \begin{eqnarray*}\left\{\begin{gathered}L\frac{di}{dt}+ri+V_c=R_ni\\i=C\frac{dV_c}{dt}\end{gathered}\right.\Rightarrow \left\{\begin{gathered}\frac{d^2V_C}{dt^2}+\frac{r-R_n}{L}\frac{dV_C}{dt}+\omega_0^2V_C=0 ;\quad \omega_0^2=\frac{1}{LC}\\\frac{d^2i}{dt^2}+\frac{r-R_n}{L}\frac{di}{dt}+\omega_0^2i=0\\ R_n<r\Rightarrow \underbrace{V_c=A\exp\left(\frac{-\omega_0t}{2Q_1}\right)\cos(\omega t+\varphi)}_{\text{regime pseudo – periodique amorti}} ;\quad Q_1=\frac{L\omega_0}{(r-R_n)} ;\quad\omega=\omega_0\sqrt{1-\frac{1}{4Q_1^2}}\\R_n\succapprox r\Rightarrow \underbrace{V_c=B\exp\left(\frac{\omega_0t}{2Q_2}\right)\cos(\omega t+\varphi’)}_{\text{regime pseudo-periodique amplifie}} ;\quad Q_2=\frac{L\omega_0}{(R_n-r)} ;\quad\omega=\omega_0\sqrt{1-\frac{1}{4Q_2^2}}\end{gathered}\right.\end{eqnarray*}L’amorçage des oscillations nécessite  que le régime soit pseudo- périodique amplifié comme le montre le portrait de phase de la figure ci-dessous.

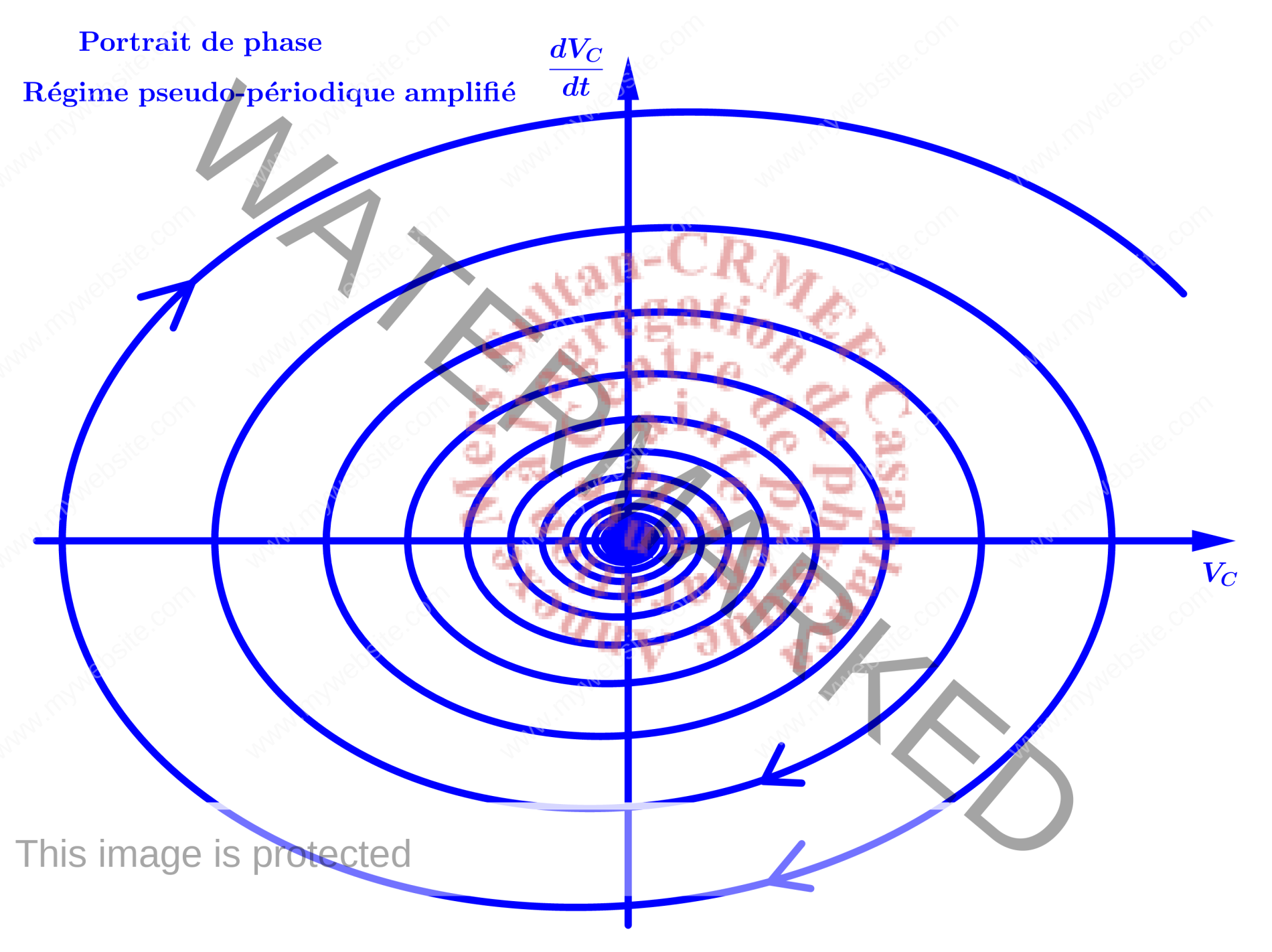
  L’amplitude ne peut pas augmenter indéfiniment. Elle est limitée par les non-linéarités dues à la saturation de l’ampli A.Op.2.

  Lorsque la résistance $R_n$ est telle que $R_n\gg r$, le régime transitoire est apériodique.

• Lorsque l’interrupteur K est fermé, l’équation différentielle du circuit devient :  \begin{eqnarray*}\left\{\begin{gathered}L\frac{di}{dt}+ri+V_c=0\\i=C\frac{dV_c}{dt}
  \end{gathered}\right.
  \Rightarrow
  \left\{\begin{gathered}\frac{d^2V_C}{dt^2}+\frac{r}{L}\frac{dV_C}{dt}+\omega_0^2V_C=0 ;\quad \omega_0^2=\frac{1}{LC}\\\underbrace{V_c=D\exp\left(\frac{-\omega_0t}{2Q_3}\right)\cos(\omega t+\varphi_3)}_{\text{regime pseudo – periodique amorti independant de Rn}} ;\quad Q_3=\frac{L\omega_0}{r} ;\quad\omega=\omega_0\sqrt{1-\frac{1}{4Q_1^2}}
  \end{gathered}\right.
  \end{eqnarray*}

2.2. Régime établi Le montage est donné dans la figure c-dessous.

On suppose que l’A.Op.2 fonctionne en régime linéaire. On peut remplacer le montage du dipôle à résistance négative par une résistance dynamique $-R_n$. L’équation différentielle du circuit s’obtient comme suit : 

\begin{eqnarray*}\left\{\begin{gathered}V_c+L\frac{di}{dt}+ri=R_ni\Downarrow\\\frac{d^2i}{dt^2}+\frac{(r-R_n)}{L}\frac{di}{dt}+\omega_0^2i=0\\\frac{d^2V_c}{dt^2}+\frac{(r-R_n)}{L}\frac{dV_c}{dt}+\omega_0^2V_c=0\\V_s=(R_n+R’)i=C(R_n+R’)\frac{dV_c}{dt}\end{gathered}\right.\Rightarrow\left\{\begin{gathered} \frac{d}{dt}\left(\frac{CV_c^2}{2}+\frac{Li^2}{2}\right)=(R_n-r)i^2\\\bullet\quad R_n<r\Rightarrow\text{amortissement des oscillations du a la perte d’energie}\\\bullet \quad R_n=r\Rightarrow \text{pas de demarrage des oscillations car il n’y pas d’energie initiale dans le systeme}\\\bullet\quad R_n\succapprox r\Rightarrow \underbrace{\frac{d^2V_c}{dt^2}+\omega_0^2V_c=0}_{\text{Oscillations quasi-sinusoidales de frequence }\frac{1}{2\pi\sqrt{LC}}\text{limitees par les saturations de l’A.Op.}}\\\bullet \quad R_n>>r\Rightarrow\text{Oscillateur de relaxation}\end{gathered}\right.\end{eqnarray*}