• La mise en évidence expérimentale de la biréfringence linéaire naturelle,
• les états de polarisation des rayons ordinaire et extraordinaire. 

Montage expérimental

surface des indices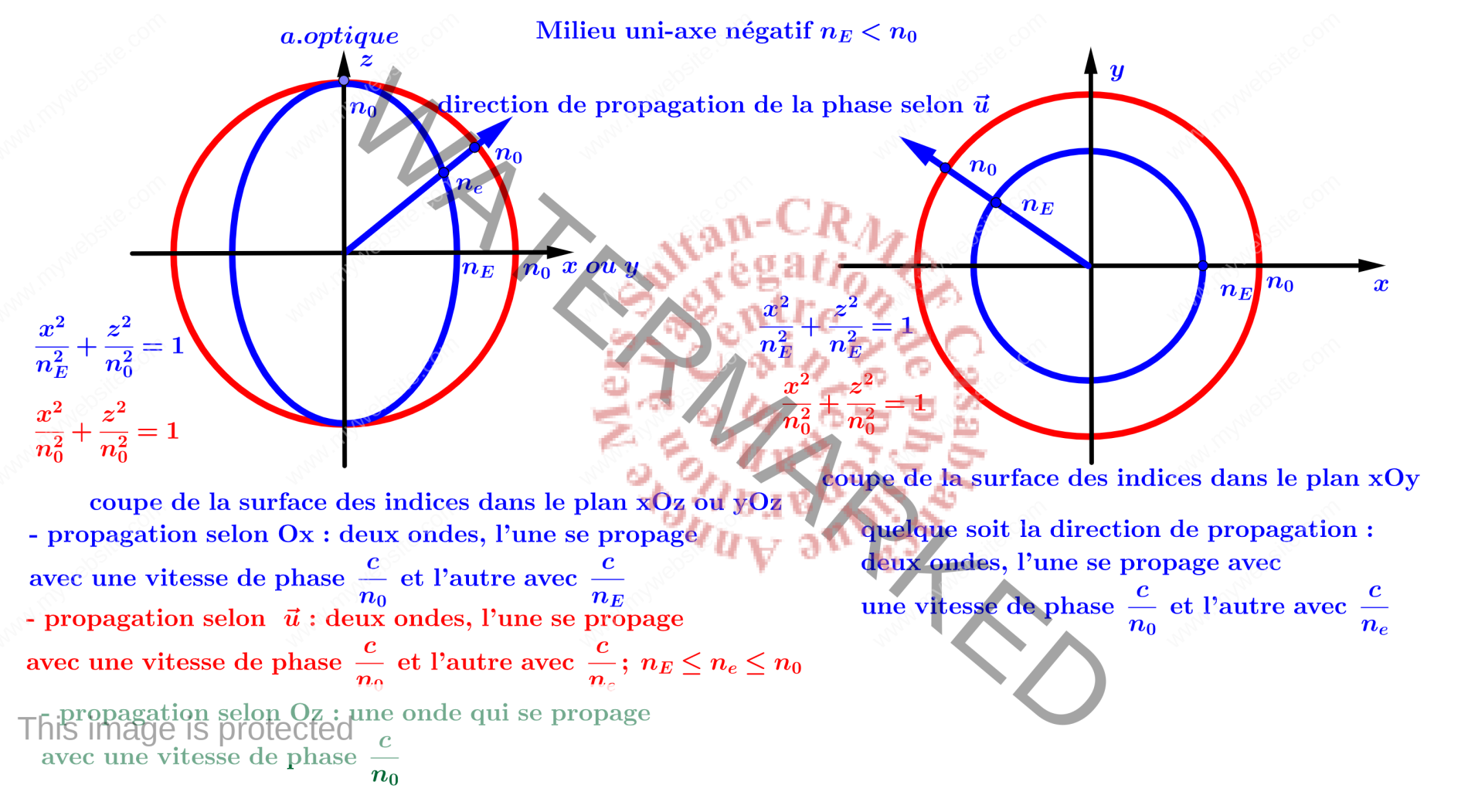

Ellipsoïdes des indices

Pour une direction du vecteur d’onde $\overrightarrow k$ d’une OPPM donnée, les états de polarisation sont portés par les axes de l’ellipse d’intersection du plan perpendiculaire à $\overrightarrow k$ et de l’ellipsoïde d’indice. Une onde est qualifiée d’ordinaire et se propage avec la vitesse de phase $\frac{c}{n_0}$ et l’autre est qualifiée d’extraoridnaire et se propage avec la vitesse de phase $\frac{c}{n_e}$ avec $n_0\leq n_e\leq n_E$. Le champ électrique est perpendiculaire au plan tangent à l’ellipsoïde des indices.

• Lampe quartz-iode,
• fente circulaire,
• rhomboèdre de spath,
• lentille convergente f’=10cm,
• diaphragme circulaire,
• polariseur,
• écran.

1. Définition Un matériau présente la biréfringence linéaire si son indice optique dépend de la direction de propagation et de l’état de polarisation de l’onde. Ce matériau présente la double réfraction : un rayon lumineux incident donne lieu à deux rayons réfracté. on distingue deux types de matériaux :

• les matériaux biréfringents uni-axe sont caractérisés par un seul axe optique,
• les matériaux biréfringents bi-axe possèdent deux axes optiques.

4. Construction d’Huygens 4.1. Interface air $(n_1)$/Milieu($n_0,n_E$)

• on considère une source ponctuelle O située à l’interface air/milieu au point d’incidence,
• on trace le demi-cercle $\mathcal C_1$ de centre O et de rayon $\frac{1}{n_1}$ dans le milieu,
• on prolonge le rayon incident jusqu’à ce qu’il rencontre $\mathcal C_1$ en un point $M_1$,
• on trace la tangente à $\mathcal C_1$ en $M_1$. Soit I le point d’intersection de cette tangente avec l’interface,
• on trace le demi-cercle $\mathcal C_2$ de centre O et de rayon $\frac{1}{n_0}$ dans le milieu,
• on trace la tangente à $\mathcal C_2$ qui passe par le point I à l’interface. Soit $M_0$ le point d’intersection de cette tangente à $\mathcal C_2$, le rayon ordinaire réfracté dans le milieu passe par O et $M_0$,
• pour tracer le rayon extraordinaire réfracté, on suppose que le milieu est uni-axe négatif et que l’axe optique n’est ni parallèle ni perpendiculaire à l’interface,
• on trace l’ellipse $\mathcal E$ de demi-grand axe $\frac{1}{n_E}$ et demi-petit axe $\frac{1}{n_0}$, on trace la tangente à l’ellipse passant par le point I de l’interface. Soit $M_e$ le point d’intersection. Le rayon extraordinaire réfracté passe par O et par $M_e$.

4.2. Milieu($n_0,n_E$)/Interface air $(n_1)$ 4.2.1. Rayon ordinaire

• on prolonge le rayon extraordinaire réfracté jusqu’à l’interface Milieu/air. Soit J le point d’incidence.
• on trace l’ellipse $\mathcal E$ de demi-grand axe $\frac{1}{n_E}$ et demi-petit axe $\frac{1}{n_0}$,
• on prolonge le rayon incident jusqu’à ce qu’il rencontre l’ellipse $\mathcal E$ en un point $L_e$,
• on trace la tangence à $\mathcal E$ en $L_e$. Cell-ci coupe l’interface Milieu/air en un point H,
• on trace le demi-cercle $\mathcal C_1$ de centre J et de rayon $\frac{1}{N_1}$,
• on trace la tangente à $\mathcal C_1$ passant par H. Soit $M_1$ le point d’intersection de cette tangente avec $\mathcal C_1$. Le rayon extraordinaire réfracté passe par J et $M_1$.