• action d’une lame demi-onde sur une polarisation rectiligne, 
• action d’une lame demi-onde sur une polarisation circulaire,
• simulation expérimentale du polarimètre de Laurent,
• action d’une lame quart d’onde sur une polarisation rectiligne ,
• analyse d’une lumière polarisée elliptiquement, 
• analyse d’une lumière polarisée circulairement.

Montage expérimental(action d’une lame demi-onde sur une polarisation rectiligne)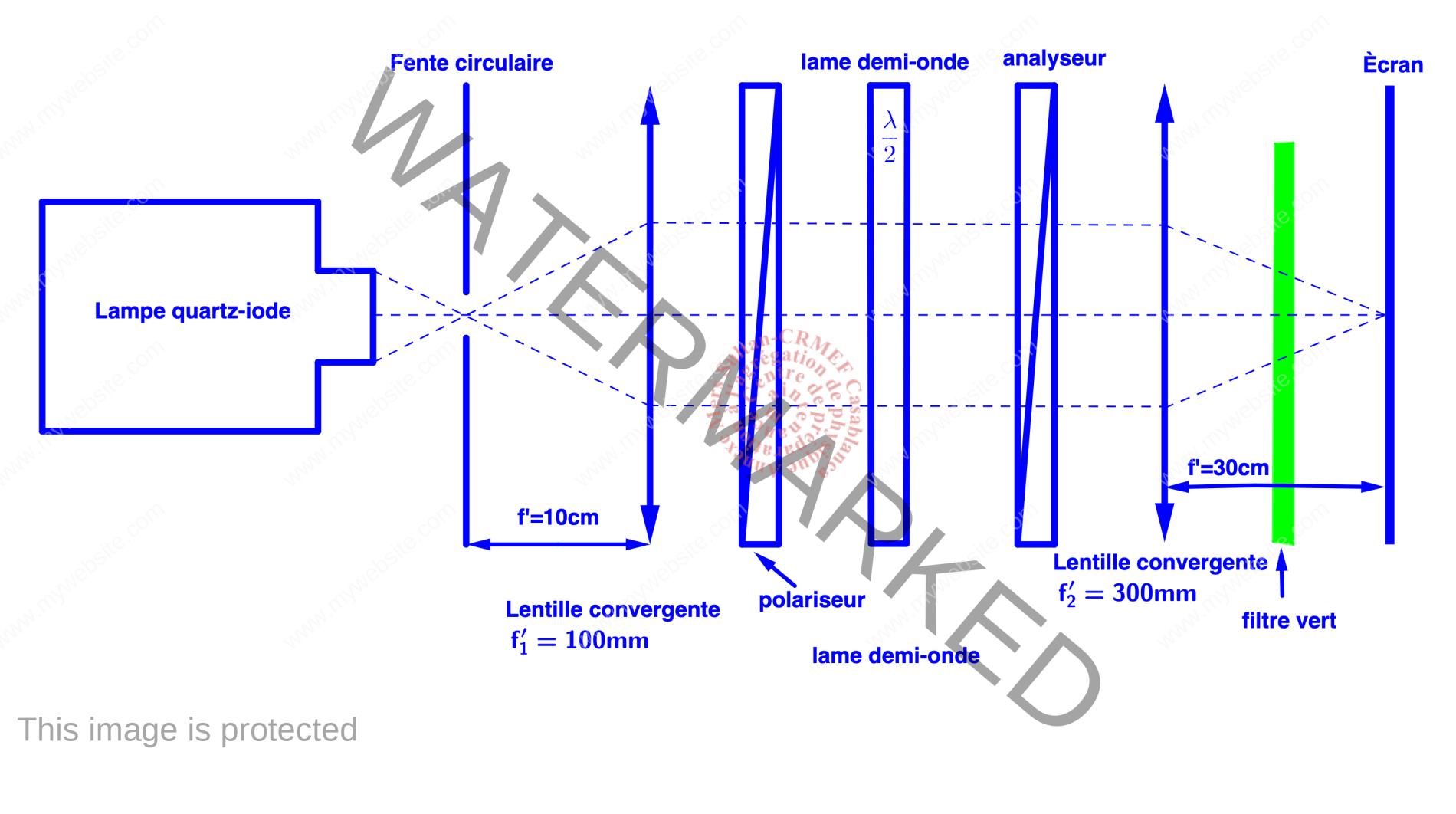Montage expérimental(simulation expérimentale du polarimètre de Laurent)

Montage expérimental(production d’une lumière polarisée elliptique et circulaire à l’aide de la lame quart d’onde)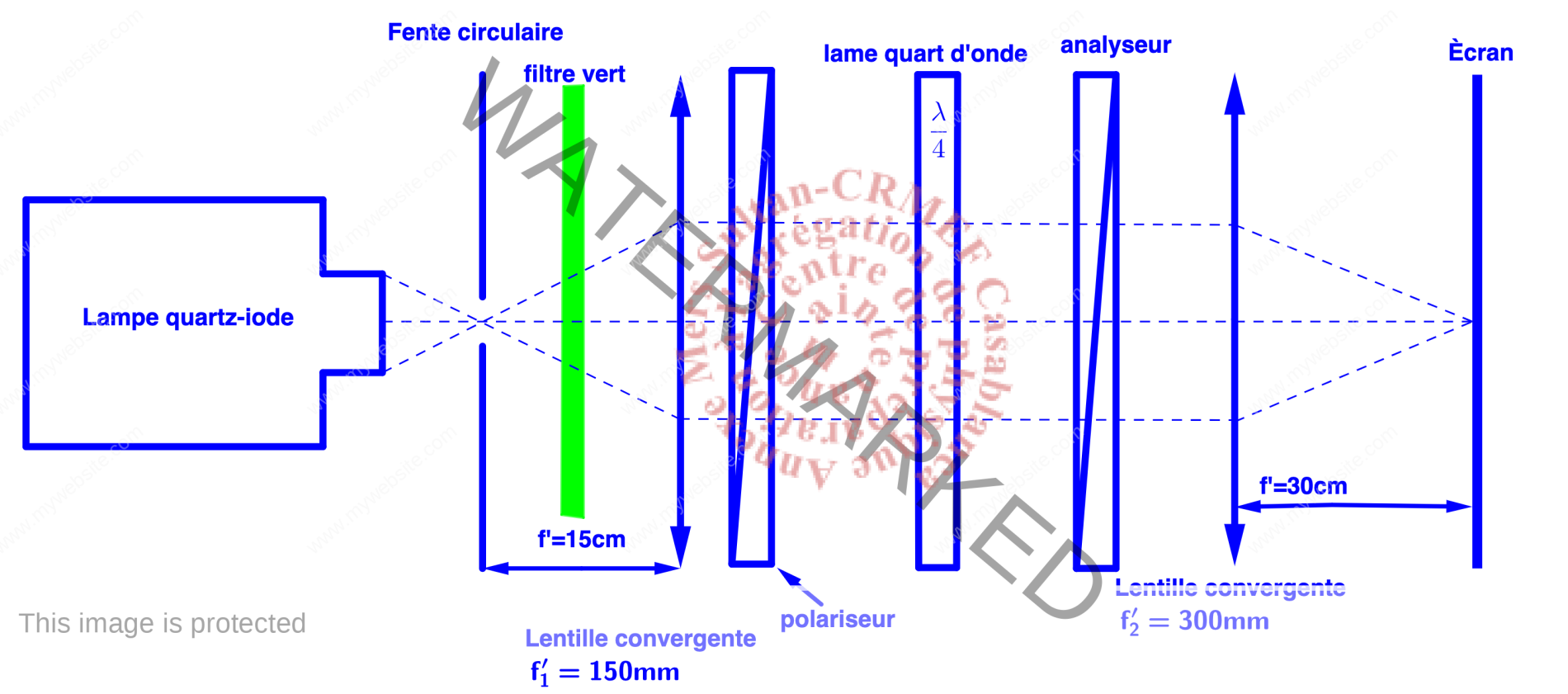

• Lentilles, f’=10 cm, f’=15cm, f’=20cm,  f’=30cm,
• diaphragme circulaire,
• lampe quartz-iode,
• polariseurs,
• Analyseur à pénombre,
• lames demi-onde,
• lames quart d’onde,
• filtre vert,
• écran.

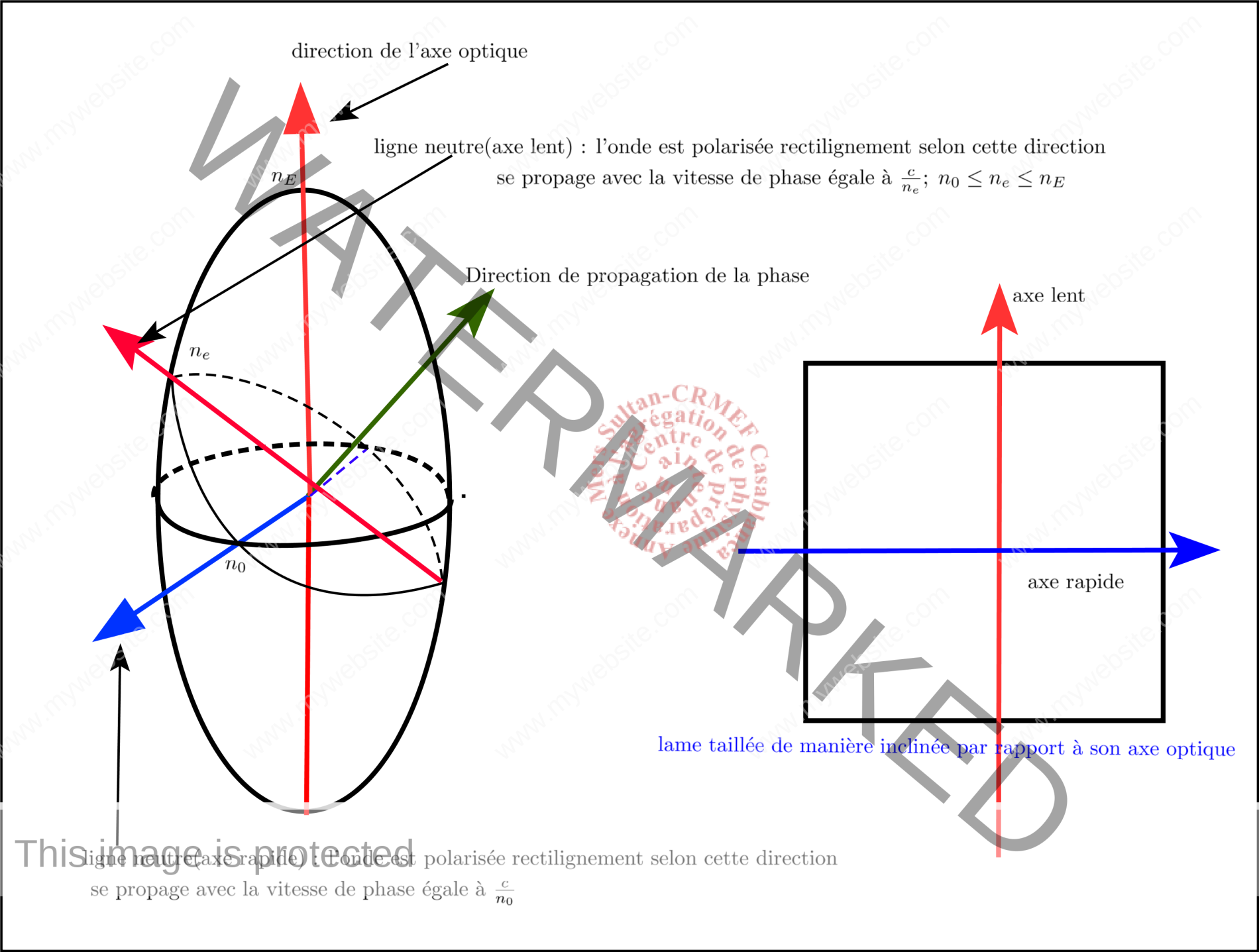
1. Lame demi-onde, simulation expérimentale du polarimètre de laurent 1.1. Lame demi-onde 1.1.1. DéfinitionC’est une lame à faces parallèles d’un matériau biréfringent uni-axe généralement le quartz taillée parallèlement à son axe optique. Une propriété caractéristique de ces matériaux c’est que pour chaque direction de propagation, il existe deux ondes ayant des polarisation rectilignes orthogonales et se propagent avec des vitesses de phase égales respectivement à $\frac{c}{n_0}$ et $\frac{c}{n_E}$. On appelle ces directions les lignes neutres de la lame pour la direction de propagation considérée. Une ligne est qualifiée d’axe lent (vitesse de phase égale à $\frac{c}{n_E}$) et l’autre est qualifiée d’axe rapide (vitesse de phase égale à $\frac{c}{n_0}$). La lame demi-onde introduit un déphasage $\phi$ entre les deux ondes extraordinaire et ordinaire tel que : $\phi=\frac{2\pi}{\lambda}(n_E-n_0)=\pi[2\pi]$ où $n_e$ représente l’indice extraordinaire et $n_0$ l’indice ordinaire du matériau dont est fabriqué la lame demi-onde.

1.1.2. Action d’une lame demi-onde sur une polarisation rectiligne incidenteLe montage expérimental utilisé est donné dans la figure ci-dessous.

• La première lentille permet d’avoir un faisceau parallèle, la deuxième lentille réalise l’image de la fente circulaire dans son plan focal image,
• le filtre vert est adapté à la lame demi-onde permet de travailler en lumière quasi-monochromatique.

Il s’agit de calculer l’amplitude complexe du vecteur excitation électrique à la sortie de l’analyseur : \begin{eqnarray*}\small\left\{\begin{gathered}\overrightarrow{\underline D}_1=\binom{D_0}{0}_{/(x,y)}=\binom{D_0\cos(\theta)}{-D_0\sin(\theta)}_{(x_L,y_L)}\\
\phi=\frac{2\pi\Delta n e}{\lambda}=\pi\Downarrow\\
\underbrace{\overrightarrow{\underline D}_2=\exp\left(i\frac{2\pi}{\lambda}n_0e\right)\binom{D_0\cos(\theta)\exp\left(i\frac{2\pi}{\lambda}\Delta ne\right)}{-D_0\sin(\theta)}_{(x_L,y_L)}=\exp\left(i\frac{2\pi}{\lambda}n_0e\right)\binom{-D_0\cos(\theta)}{-D_0\sin(\theta)}_{(x_L,y_L)}=\exp\left(i\frac{2\pi}{\lambda}n_0e\right)\binom{-D_0\cos(2\theta)}{-D_0\sin(2\theta)}_{(x,y)}}_{\text{La lame demi-onde tourne la polarisation rectiligne incidente d’un angle egale a }2\theta}\\\overrightarrow{\underline D}_3=-D_0\exp\left(i\frac{2\pi}{\lambda}n_0e\right)\sin(2\theta)\Rightarrow I_{transmise}=I_0\sin^2(2\theta)\\
\underbrace{\theta=0\quad \text{ et }\theta=\frac{\pi}{2}\Rightarrow I_{transmise}=0}_{\text{les lignes neutres coincident avec les directions privilegiees du polariseur et de l’analyseur}}
\end{gathered}\right.\end{eqnarray*}Ainsi on montre que la lame demi-onde transforme une polarisation rectiligne en une polarisation rectiligne symétrique par rapport à ces lignes neutres (rotateur de polarisation).1.2. Simulation expérimentale du polarimètre de Laurent Le montage utilisé est donné dans la figure ci-dessous.

• la première lentille permet d’obtenir un faisceau parallèle,
• la deuxième lentille conjugue l’analyseur à pénombre avec l’écran, l’analyseur sert à analyser la polarisation rectiligne issue de l’analyseur à pénombre,
• L’analyseur à pénombre est constitué d’un polariseur et d’une lame demi-onde collée sur la moitié du polariseur. On suppose que la lame demi-onde se trouve dans la moitié supérieure telle que l’angle entre la direction privilégiée du polariseur est $\varepsilon\approx 1^\circ$ comme le montre le schéma suivant. La polarisation à la sortie du polariseur $P_B$ est transformée en son symétrique par rapport à l’axe lent et devient $P_H$ pour la moitié supérieure. Pour la moitié inférieure, la polarisation est portée par $P_B$. L’intensité transmise dans la moitié supérieure est donnée par : $I_H=I_0\cos^2\left(\frac{\pi}{2}+\varepsilon\right)=I_0\sin^2(\varepsilon)=I_0\varepsilon^2$L’intensité transmise par la moitié inférieure s’exprime sous la forme : $I_B=I_0\cos^2\left(\frac{\pi}{2}\varepsilon\right)=I_0\sin^2(\varepsilon)=I_0\varepsilon^2$ $I_H=I_B=I_0\varepsilon^2$ : traduit l’équi-pénombre des demi-plages supérieure et inférieure
• on commence par chercher l’équi-pénombre des demi-plages en tournant l’analyseur dans son plan,
• ensuite, on introduit un rotateur de polarisation qui peut être une lame demi-onde ou un milieu actif,
• puis on tourne l’analyseur d’un angle $\theta$ pour rétablir l’équi-pénombre des demi-plages.

2. Lame quart d’onde 2.1. Définition C’est une lame à faces parallèles d’un matériau biréfringent uni-axe généralement le quartz taillée parallèlement à son axe optique. Une propriété caractéristique de ces matériaux c’est que pour chaque direction de propagation, il existe deux ondes ayant des polarisations rectilignes orthogonales et se propagent avec des vitesses de phase égales respectivement à $\frac{c}{n_0}$ et $\frac{c}{n_e}$ où $n_0\leq n_e\leq n_E$. On appelle ces directions les lignes neutres de la lame pour la direction de propagation considérée. Une ligne est qualifiée d’axe lent (vitesse $\frac{c}{n_e}$) et l’autre est qualifié d’axe rapide (vitesse $\frac{c}{n_0}$). La lame demi-onde introduit un déphasage de $\frac{\pi}{2}$ entre les deux ondes. 2.2. Action d’une lame taillée parallèlement à son axe optique sur une polarisation rectiligne Considérons le schéma ci-contre. Le champ électrique à la sortie du polariseur s’exprime sous la forme : $\overrightarrow E_p=\binom{E_0\cos(\omega t)}{0}_{/(x,y)}=\binom{E_0\cos(\alpha)\cos(\omega t)}{E_0\sin(\alpha)\cos(\omega t)}_{/(x_L,y_L)}$
Le champ électrique à la sortie de la lame est donné par : \begin{eqnarray*}\left\{\begin{gathered}\overrightarrow E_L=\binom{a\cos(\omega t-\phi_x)}{b\cos(\omega t-\phi_y)}_{/(x_L,y_L)}\\ a=E_0\cos(\alpha) ;\quad b=E_0\sin(\alpha)\\ \phi=\phi_y-\phi_x ;\quad \omega t’=\omega t-\phi_x\end{gathered}\right.\Rightarrow \overrightarrow E_L=\binom{a\cos(\omega t)}{b\cos(\omega t-\phi)}_{/(x_L,y_L)}\end{eqnarray*}On distingue deux cas :

• $\phi>0\Rightarrow \phi_y>\phi_x$ : l’axe $(Ox_L)$ est appelé axe rapide et l’axe $(Oy_L)$ est l’axe lent,
• $\phi<0\Rightarrow \phi_x>\phi_y$ : l’axe $(Oy_L)$ est appelé axe rapide et l’axe $(Ox_L)$ est l’axe lent

• $\phi=0$ : lame onde. La polarisation rectiligne incidente n’est pas modifiée par la lame. L’équation de la droite est : $Y_L=\frac{b}{a}x_L$,
• $\phi=\pm \pi$ : lame demi-onde. L’équation décrite par l’extrémité du champ électrique est de la forme : $Y_L=-\frac{b}{a}x_L$. 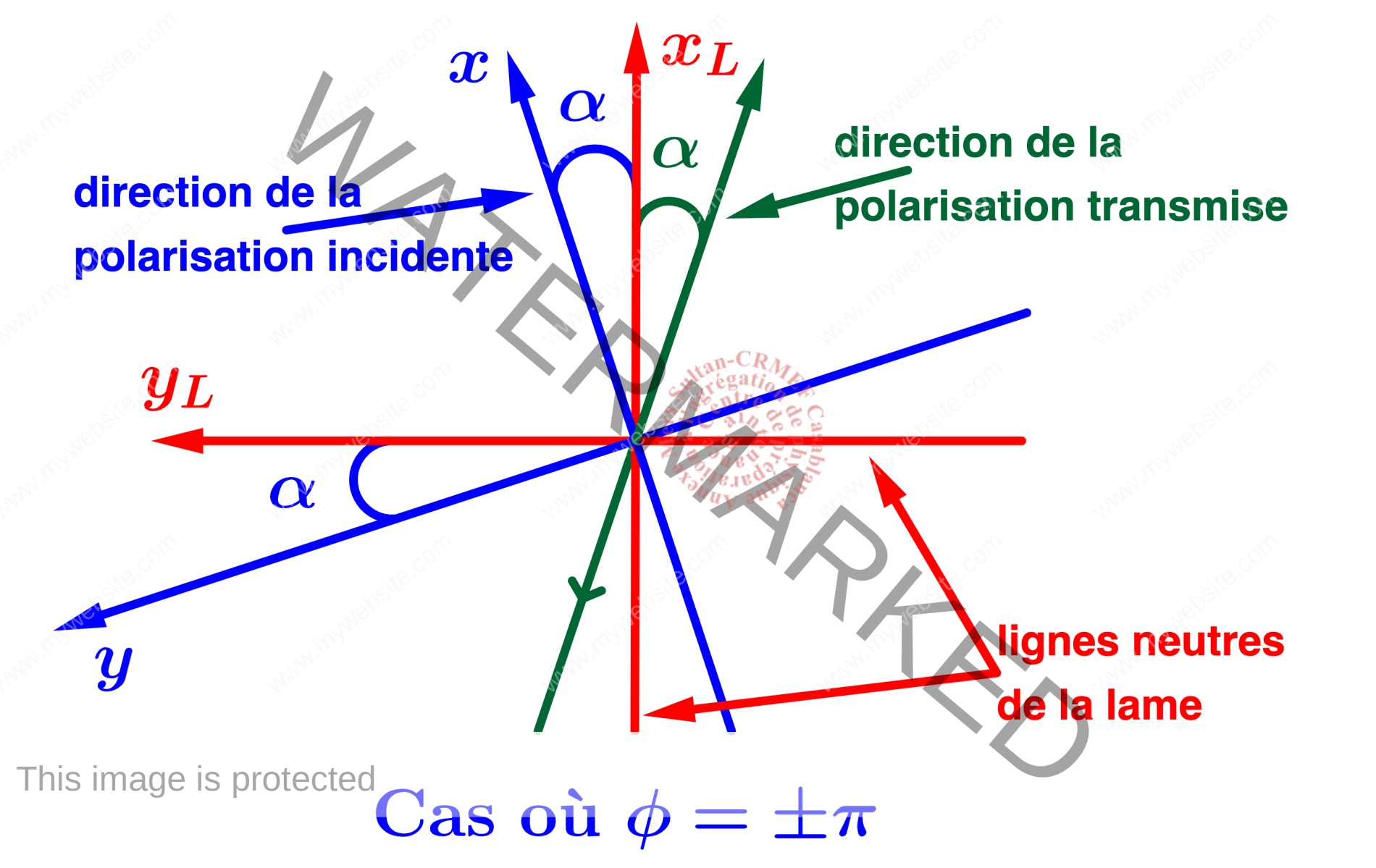La lame a transformé la polarisation rectiligne incidente en une polarisation rectiligne symétrique par rapport aux lignes neutres de la lame,
• $\phi=\frac{\pi}{2}$ : lame quart d’onde. L’équation décrite par l’extrémité du champ électrique devient : $\frac{x_L^2}{a^2}+\frac{y_L^2}{b^2}=1$  C’est une ellipse dont les axes sont confondus avec les lignes neutres de la lame quart d’onde.
•   Dans le cas où $\alpha\in[\pi/4,\pi/2]$, la polarisation transmise est une ellipse gauche de demi-grand axe $(Oy_L)$

• cas où $\phi=\frac{-\pi}{2}$ : lame quart d’onde. L’équation décrite par l’extrémité du champ électrique devient : $\frac{x_L^2}{a^2}+\frac{y_L^2}{b^2}=1$ C’est une ellipse dont les axes sont confondus avec les lignes neutres de la lame quart d’onde.

• Dans le cas où $\alpha\in[\pi/4,\pi/2]$, la polarisation transmise est une ellipse droite de demi-grand axe $(Oy_L)$,
• le sens de l’ellipse est celui qui ramène la direction de polarisation rectiligne incidente vers la direction de l’axe lent de la lame quart d’onde.

• Cas général : $\phi\neq0$, $\phi\neq\pm\pi$ et $\phi\neq\pm\frac{\pi}{2}$ Dans ce cas les axes de l’ellipse dépendent du déphasage $\phi$. Soient $(x_e,y_e)$ les axes de l’ellipse comme le montre la figure ci-contre. L’équation de l’ellipse dans le système d’axes $(x_e,y_e)$ s’exprime sous la forme : $\frac{x_e^2}{A^2}+\frac{y_e^2}{B^2}=1$ A et B se déterminent en utilisant les relations de passage de $(x_L,y_L)$ à $(x_e,y_e)$ : \begin{eqnarray*}\left\{\begin{gathered}x_L=x_e\cos(\beta)-y_e\sin(\beta)\\ y_L=x_e\sin(\beta)+y_e\cos(\beta)\\\frac{x_L^2}{a^2}+\frac{y_L^2}{b^2}-\frac{2x_Ly_L}{ab}\cos(\phi)=\sin^2(\phi)\end{gathered}\right.\Downarrow \\\left\{\begin{gathered}\frac{1}{A^2}=\frac{1}{\sin^2(\phi)}\left[\frac{\cos^2(\beta)}{a^2}+\frac{\sin^2(\beta)}{b^2}-\frac{\sin(2\beta)\cos(\phi)}{ab}\right]\\ \frac{1}{B^2}=\frac{1}{\sin^2(\phi)}\left[\frac{\cos^2(\beta)}{b^2}+\frac{\sin^2(\beta)}{a^2}+\frac{\sin(2\beta)\cos(\phi)}{ab}\right]\\\sin(2\beta)\left(\frac{1}{b^2}-\frac{1}{a^2}\right)-\frac{\cos(2\beta)\cos(\phi)}{ab}=0\end{gathered}\right.\end{eqnarray*}