Couplage capacitif
Obtenir la courbe de résonance de deux circuits rLC identiques couplés par une capacité :
-
-
à l’aide de la détection de crête sans seuil,
-
-
[peekaboo_content]
-
à l’aide de la détection numérique faisant intervenir la transformée de Hilbert,
- à l’aide de la réponse impulsionnelle,
- à l’aide de la réponse indicielle. [/peekaboo_content]
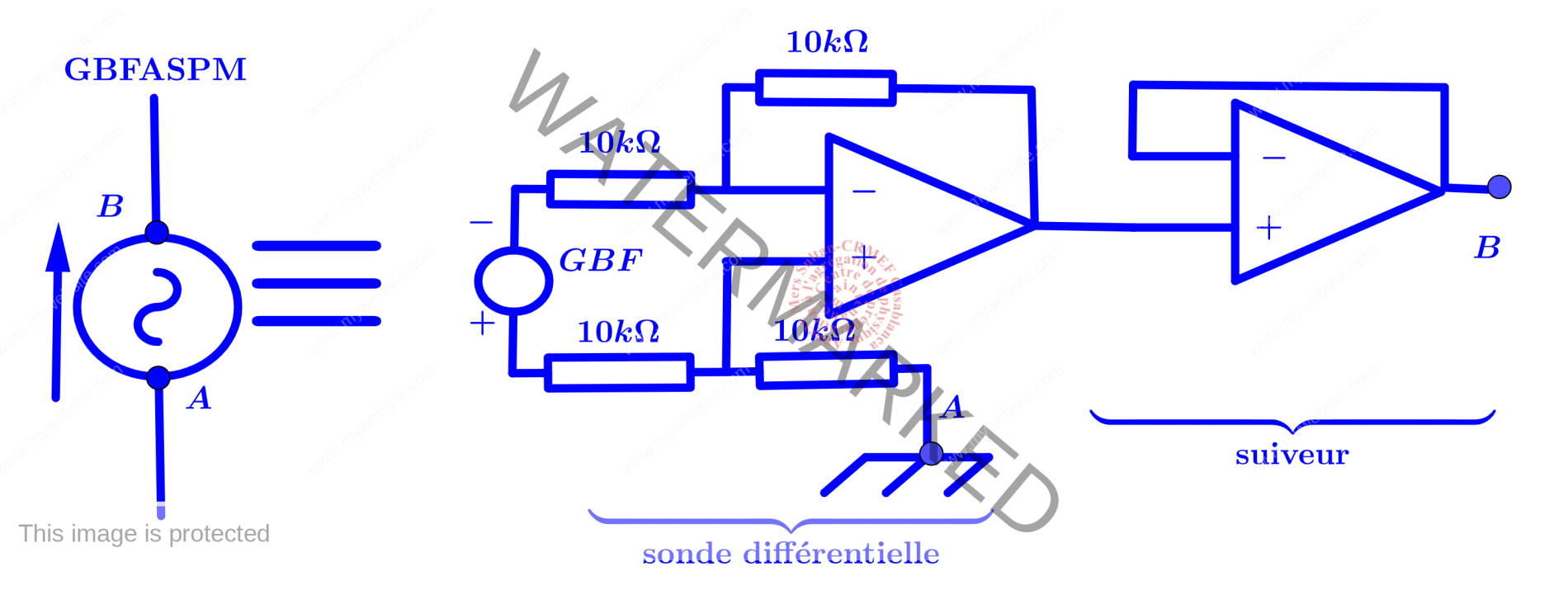
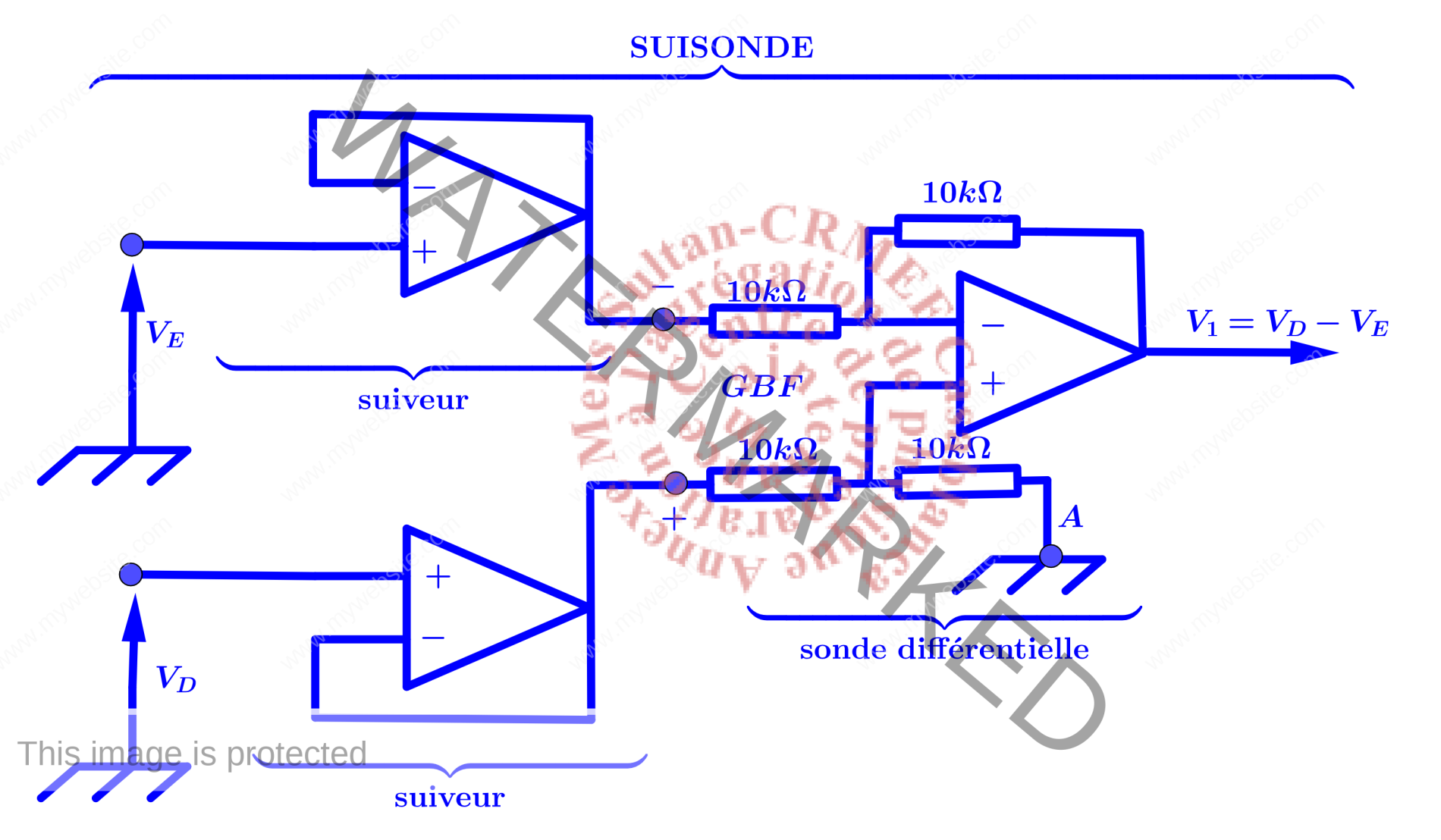
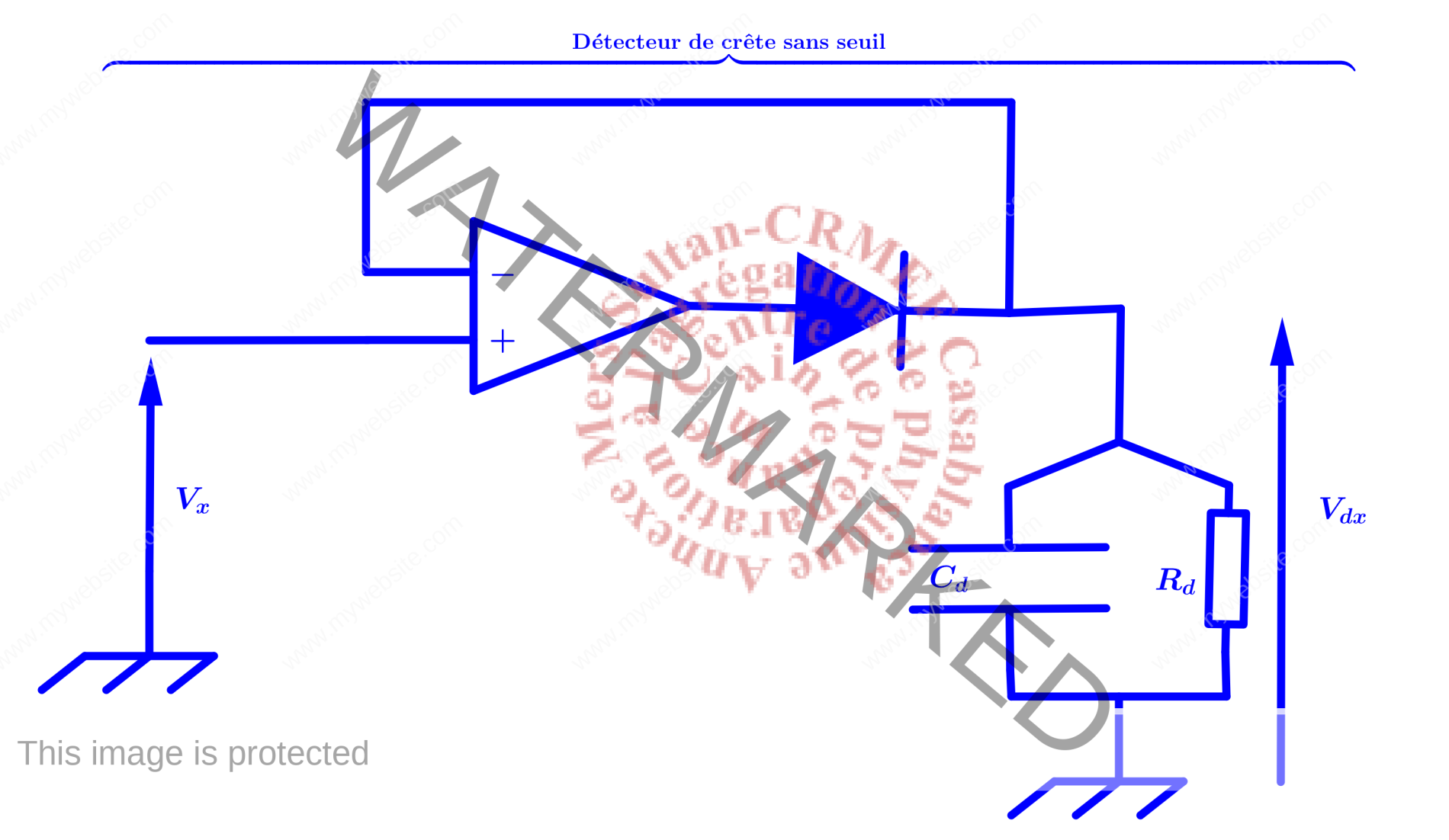
Montage expérimental (courbes de résonance à l’aide de la détection de crête)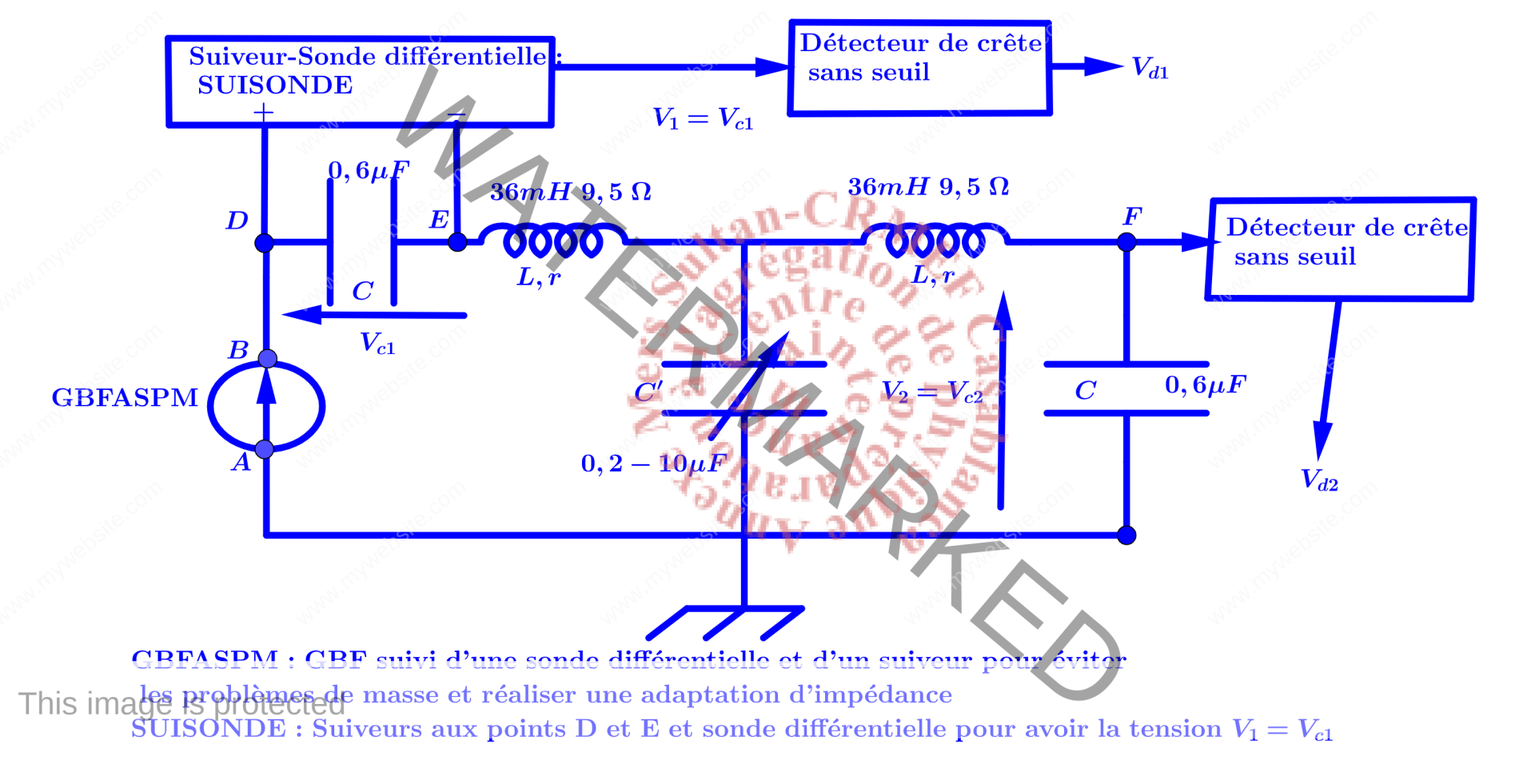
 [peekaboo_content] Montage expérimental(courbe de résonance à l’aide de la transformée de Hilbert, à l’aide la réponse impulsionnelle et à l’aide la réponse indicielle.)
[peekaboo_content] Montage expérimental(courbe de résonance à l’aide de la transformée de Hilbert, à l’aide la réponse impulsionnelle et à l’aide la réponse indicielle.)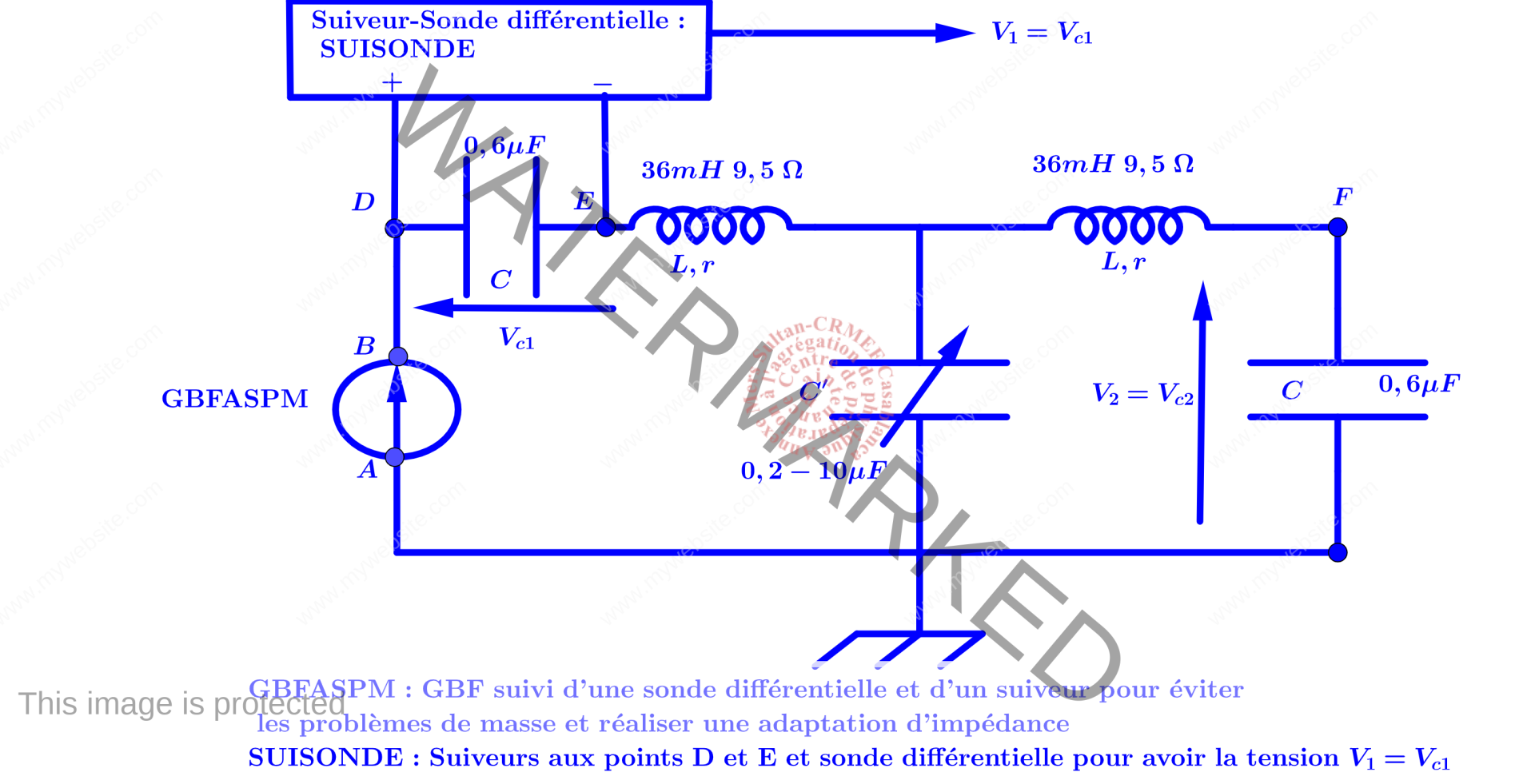
[/peekaboo_content]
- Carte d’acquisition+PC,
- oscilloscopes,
boites à décades de capacités,
deux bobines,
- GBF,
ampli. Op. TL081,
résistances 10k$\Omega$,
fils électriques
1. Courbes de résonance à l’aide du détecteur de crête
On considère le schéma synoptique donné dans la figure ci-dessous.La tension $V_{AB}=V_{GBF}$ est une tension sinusoïdale. On se place dans le régime sinusoïdal forcé.



L’expression des amplitudes complexes des tensions $V_1$ et $V_2$ s’obtiennent comme suit :\begin{eqnarray*}\left\{\begin{gathered}\underbrace{(\underline V_1+\underline V_2)-LC\omega^2(\underline V_1+\underline V_2)+jrC\omega(\underline V_1+\underline V_2) =\underline V_{GBF}}_{\text{loi des mailles D-E-F-G-H-A-B}}\\\underbrace{jC\omega\underline V_1=jC’\omega \underline V_F+jC\omega \underline V_2 \Rightarrow \underline V_1=\underline V_2+\frac{C’}{C}\underline V_F}_{\text{loi des noeuds en F}}\\ \underbrace{\underline V_F=\underline V_2-LC\omega^2\underline V_2+jrC\omega \underline V_2}_{\text{loi des mailles F-G-H-F}}\end{gathered} \right.\end{eqnarray*}On pose :
\begin{eqnarray*}\underline S=\underline V_1+\underline V_2 ;\quad\underline D=\underline V_1-\underline V_2\Rightarrow \underline V_1=\frac{\underline S+\underline D}{2} ;\quad \underline V_1=\frac{\underline S-\underline D}{2}\end{eqnarray*}
les équations deviennent : \begin{eqnarray*}\left\{\begin{gathered} \underline S\left[1-LC\omega^2+jrC\omega\right]=\underline V_{GBF}\quad\quad(eq1)\\\underline D\left[2+\frac{C’}{C}-LC’\omega^2+jrC’\omega\right]+\underline S\left[LC’\omega^2-\frac{C’}{C}-jrC’\omega\right]=0\quad\quad(eq2)\\\frac{C’}{C}\times(eq1)+(eq2) \Rightarrow \underline D\left[1-\frac{LCC’\omega^2}{2C+C’}+\frac{jrCC’\omega}{2C+C’}\right]=\frac{C’}{2C+C’}\underline V_{GBF}\\\omega_1^2=\frac{1}{LC} ;\quad \omega_2^2=\frac{2C+C’}{LCC’}=\omega_1^2\left(1+\frac{2C}{C’}\right) ;\quad Q_1=\frac{L\omega_1}{r} ;\quad Q_2=\frac{L\omega_2}{r}\Downarrow\\ \underline S=\frac{\underline V_{GBF}}{1-\frac{\omega^2}{\omega_1^2}+j\frac{\omega}{Q_1\omega_1}} ;\quad \underline D=\frac{\underline V_{GBF}}{1-\frac{\omega^2}{\omega_2^2}+j\frac{\omega}{Q_2\omega_2}}\times \frac{C’}{2C+C’}\Downarrow\\|\underline S|=\frac{|\underline V_{GBF}|}{\sqrt{(1-x_1^2)^2+\frac{x_1^2}{Q_1^2}}} ;\quad |\underline D|=\frac{|\underline V_{GBF}|}{\sqrt{(1-x_2^2)^2+\frac{x_2^2}{Q_2^2}}}\times \frac{C’}{2C+C’} ;\quad x_1=\frac{\omega}{\omega_1} ;\quad x_2=\frac{\omega}{\omega_2}\end{gathered} \right.\end{eqnarray*}La résonance des amplitudes de S et D a lieu lorsque $Q_1$ et $Q_2$ sont supérieures à $\frac{1}{\sqrt{2}}$. Les pulsations de résonance sont données par :
\begin{eqnarray*}\left\{\begin{gathered}\underbrace{\omega_{\rm res1}=\omega_1\sqrt{1-\frac{1}{2Q_1^2}}\approx \omega_1\text{ lorsque }Q_1^2\gg 1/2}_{\text{resonance de l’amplitude de S}}\\ \underbrace{\omega_{\rm res2}=\omega_2\sqrt{1-\frac{1}{2Q_2^2}}\approx \omega_2\text{ lorsque }Q_2^2\gg 1/2}_{\text{resonance de l’amplitude de D}}\end{gathered} \right.\end{eqnarray*}Les amplitudes complexes des tensions $V_1$ et $V_2$ sont données par :
\begin{eqnarray*}\left\{\begin{gathered} \underline V_1=\frac{\underline S+\underline D}{2}=\frac{\underline V_{GBF}}{2}\left[\frac{1}{1-\frac{\omega^2}{\omega_1^2}+j\frac{\omega}{Q_1\omega_1}}+\frac{C’}{2C+C’}\frac{1}{1-\frac{\omega^2}{\omega_2^2}+j\frac{\omega}{Q_2\omega_2}}\right]\\ \underline V_2=\frac{\underline S-\underline D}{2}=\frac{\underline V_{GBF}}{2}\left[\frac{1}{1-\frac{\omega^2}{\omega_1^2}+j\frac{\omega}{Q_1\omega_1}}-\frac{C’}{2C+C’}\frac{1}{1-\frac{\omega^2}{\omega_2^2}+j\frac{\omega}{Q_2\omega_2}}\right]\end{gathered} \right.\end{eqnarray*}
Les amplitudes de $V_1$ et $V_2$ présentent deux pics de résonance aux pulsations $\omega_1$ et $\omega_2$ lorsque $Q_1^2\gg 1/2$ et $Q_2^2\gg 1/2$. Dans ce cas la fréquence de résonance $f_1$ est indépendante de la capacité du couplage C’ : \begin{eqnarray*}f_1=\frac{1}{2\pi\sqrt{LC}}\end{eqnarray*}Par contre la fréquence de résonance $f_2$ est fortement liée à la capacité C’ : \begin{eqnarray*}f_2=\frac{1}{2\pi\sqrt{LC}}\sqrt{1+\frac{2C}{C’}}=f_1\sqrt{1+\frac{2C}{C’}}\end{eqnarray*}
- Lorsque le couplage est faible(C’ est très grande par rapport à C), $f_2\approx f_1$,
- lorsque $2C\gg C’$(fort couplage) : $f_2\approx f_1\sqrt{\frac{2C}{C’}}$ dépend fortement avec C’
[peekaboo_content]2. Courbes de résonance à l’aide de la détection d’enveloppe numérique faisant intervenir la transformée de Hilbert
2.1. Définition et propriétés
La transformée de Hilbert $H(x(t))=\widetilde{x}(t)$ d’une fonction réelle x(t) est définie par :\begin{eqnarray*}\widetilde{x}(t)=f(t)\otimes\frac{1}{\pi t}=\frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{x(\tau)}{t-\tau}d\tau\end{eqnarray*}où $\otimes$ représente le produit de convolution. En raison d’une singularité possible à $t = \tau$, l’intégrale doit être considérée comme la valeur principale de Cauchy : \begin{eqnarray*}\widetilde{x}(t)=\frac{1}{\pi}\lim\limits_{\varepsilon \rightarrow 0} \left\{\int_{-\infty}^{-\varepsilon}\frac{x(\tau)}{t-\tau}d\tau+\int_{+\varepsilon}^{+\infty}\frac{x(\tau)}{t-\tau}d\tau\right\}\end{eqnarray*}La transformée de Hilbert peut être interprétée comme un filtre linéaire invariant dans le temps. Sa réponse impulsionnelle s’exprime par :\begin{eqnarray*}
h(t)=\widetilde{\delta(t)}=\frac{1}{\pi t}\otimes \delta(t)=\frac{1}{\pi t}\end{eqnarray*}La fonction de transfert de ce filtre (transformée de Fourier de la réponse impulsionnelle) est donnée par :\begin{eqnarray*}
H(\omega)=-j \rm sign(\omega)\end{eqnarray*}où $\rm sign$ représente la fonction signe :\begin{eqnarray*}
\rm sign(x)=\left\{\begin{gathered}+1\text{ si }x>0\\ -1\text{ si }x<0\end{gathered}\right.\end{eqnarray*}et $j$ le nombre complexe $j^2=-1$. Il s’agit d’un filtre passe-tout déphaseur de $-\frac{\pi}{2}$. \noindent
La transformée de Hilbert d’une fonction x(t) est sous forme d’un produit de convolution. Il en résulte que pour la calculer, il suffit de calculer la transformée de Fourier inverse du produit de la transformée de Fourier $X(\omega)$ par la fonction de transfert $H(\omega)=\rm -jsign(\omega)$ : \begin{eqnarray*}
\widetilde{x}(t)=\mathcal F^{-1}(\rm H(\omega)\times X(\omega)) =\mathcal F^{-1}(\rm-jsign(\omega)\times X(\omega)) \end{eqnarray*} La transformée de Hilbert vérifie les propriétés suivantes :
- linéarité : la transformée de Hilbert d’une somme est la somme des transformées de Hilbert.\begin{eqnarray*}\forall \lambda_1 \ ;\rm et\ ;\lambda_2\in\mathbb C,\widetilde{\lambda_1x_1(t)+\lambda_2x(t)}=\lambda_1\widetilde{x_1}(t)+\lambda_2\widetilde{x_2}(t)
\end{eqnarray*} - La transformée de Hilbert du produit d’une fonction basse fréquence $x_{BF}(t)$ et une fonction haute fréquence $y_{HF}(t)$ dont les spectres respectifs dont disjoints est donné par l’identité de Bedorsian :
\begin{eqnarray*}\rm \widetilde{x_{BF}(t)y_{HF}(t)}=x_{BF}(t)\widehat{y_{HF}(t)}\end{eqnarray*}
2.2. Utilité pratique : extraction de l’enveloppe et de la phase
On s’intéresse dans toute la suite aux signaux à bande étroite.2.2.1. Signal analytiqueSoit un signal réel x(t) de transformée de Fourier $X(f)$. Le signal analytique correspondant a(t) est définit par :
\begin{eqnarray*}
a(t)=x(t)+j\widetilde{x}(t)
\end{eqnarray*} Le signal réel est la partie réelle du signal analytique associé $x(t)=\mathcal{R}e(a(t))$. La transformée de Fourier du signal analytique s’exprime sous la forme : \begin{eqnarray*}
A(f)=X(f)+\rm sign(f)X(f)=\left\{\begin{gathered}2X(f)\text{ si }f>0\\0\text{ si }f<0\end{gathered}\right.
\end{eqnarray*} Le spectre du signal analytique s’identifie avec celui du signal réel dans le domaine des fréquences positives à un facteur de 2 près.2.2.2. Enveloppe complexeEn général, le spectre du signal analytique est centrée autour d’une fréquence $f_0$. On définit l’enveloppe complexe y(t) d’un signal réel à bande étroite le signal y(t) dont la transformée de Fourier Y(f) identique au spectre du signal analytique mais centré sur 0 :
\begin{eqnarray*}
Y(f)=A(f+f_0)\Rightarrow y(t)=a(t)\exp(-j2\pi f_0t)
\end{eqnarray*} L’enveloppe complexe possède comme module $|y(t)|$ et d’argument $arg(y(t))$. Il en résulte l’expression du signal réel à bande étroite :
\begin{eqnarray*}
x(t)=\mathcal Re(a(t))=|y(t)|\cos(2\pi f_0t+\rm arg(y(t)))
\end{eqnarray*} l’enveloppe complexe est un signal basse fréquence de variation lente par rapport à $f_0$. Le signal réel est un signal sinusoïdal de fréquence $f_0$ et d’amplitude $|y(t)|$ lentement variable. Ces caractéristiques sont données par :
- l’amplitude instantanée : $|y(t)|$,
- la phase instantanée : $\Psi(t)=2\pi f_0 t+\rm arg(y(t))$
- la fréquence instantanée : $f(t)=\frac{1}{2\pi}\frac{d\Psi(t)}{dt}=f_0+\frac{1}{2\pi}\frac{d\rm arg(y(t))}{dt}$
Le développement permettant d’obtenir les amplitudes complexes des tensions $\underline V_1$ et $\underline V_2$ est identique à celui du premier paragraphe.
3. Courbes de résonance à l’aide de la réponse impulsionnelle 3.1. Principe de la réponse impulsionnelle Toute fonction x(t) s’exprime à l’aide de la distribution de Dirac $\delta$ sous la forme :\begin{eqnarray*}\label{conv} x(t)=\int_{-\infty}^{+\infty}x(\tau)\delta(t-\tau)d\tau=x(t)\otimes\delta(t)\end{eqnarray*}Il s’agit d’un produit de convolution de x(t) par delta(t). Considérons un filtre linéaire et invariant dans le temps (un retard à l’entrée se manifeste par un retard identique à la sortie sans changer la forme). Soit s(t) la réponse à une entrée e(t). La réponse impulsionnelle h(t) est définie par sa réponse à une impulsion de Dirac, c’est à dire : \begin{eqnarray*}e(t)=\delta(t)\Rightarrow s(t)=h(t)=R(\delta(t))\end{eqnarray*}où R est un opérateur linéaire.\noindent Un signal quelconque e(t) est une somme infinie d’impulsions décalées. Chacune de ces impulsions engendre une sortie sous forme d’une réponse impulsionnelle décalée (le système est invariant dans le temps). Le système est linéaire, la réponse à la somme des impulsions décalées est la somme des réponses à chaque impulsion : \begin{eqnarray*}s(t)=R(e(t))=\int_{-\infty}^{+\infty}e(\tau)h(t-\tau)d\tau=e(t)\otimes h(t)\end{eqnarray*}La causalité impose une condition sur h(t) de la forme : \begin{eqnarray*}h(t)=0\text{ si } t<0\Rightarrow s(t)=\int_{-\infty}^t x(\tau)h(t-\tau)d\tau\end{eqnarray*}\begin{eqnarray*}h(t)=0\text{ si } t<0\Rightarrow s(t)=\int_{-\infty}^t x(\tau)h(t-\tau)d\tau\end{eqnarray*}La relation entrée-sortie est un produit de convolution entre l’entrée et la réponse impulsionnelle du filtre dans le domaine temporel. La transformée de Fourier de cette relation s’exprime par : \begin{eqnarray*}\widehat S(f)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}h(t-\tau)e(\tau)\exp(-j2\pi ft)d\tau dt\end{eqnarray*}En effectuant le changement de variable $t-\tau=u$ on obtient l’expression de la transformée de Fourier de la sortie sous la forme : \begin{eqnarray*}\widehat S(f)=\widehat H(f)\times \widehat E(f)\end{eqnarray*}Ainsi la relation entrée-sortie dans le domaine fréquentiel se manifeste par le produit de la transformée de Fourier de l’entrée qui est égale à 1(impulsion de Dirac) et de la fonction de transfert $H(f)$. La courbe de résonance représente le module de la fonction de transfert. Celle-ci est la transformée de Fourier de la réponse impulsionnelle du filtre.
3.2. Montage expérimental Le montage expérimental est identique à celui du paragraphe précédent. Le développement permettant d’obtenir les amplitudes complexes des tensions $\underline V_1$ et $\underline V_2$ est identique à celui du premier paragraphe.
4. Courbes de résonance à l’aide de la réponse indicielle 4.1. Principe de la réponse indicielle La réponse indicielle est la réponse à un échelon de tension $v_e(t) $ de la forme : \begin{eqnarray*}v_e=\left\{\begin{gathered}E\text{ si } t>0\\ 0\text{ si } t<0\end{gathered}\right.\end{eqnarray*}Soit $s_e(t)$ la réponse du système à l’échelon de tension $v_e$. Celle-ci vérifie les deux relations suivantes : \begin{eqnarray*}s_e(t)=\int_{-\infty}^{+\infty}v_e(\tau)h(t-\tau)d\tau\Leftrightarrow S_e(f)=H(f)\times V_f(f)\end{eqnarray*}où les symboles en majuscules représentent les transformées de Fourier des grandeurs. Lorsque $v_e=v_i=E\delta(t)$, la sortie est $s_i(t)=h(t)$. La dérivée au sens des distributions de l’échelon de tension $v_e$ est donnée par $E\delta(t)$. La transformée de Fourier de la dérivée de la réponse indicielle $s_e(t)$ est donnée par : \begin{eqnarray*}TF\left(\frac{ds_e(t)}{dt}\right)=j\omega S_e(\omega)=j\omega V_e(\omega)H(\omega)\end{eqnarray*}4.2. Montage expérimental-expressions de $\underline V_1$ et $\underline V_2$ Le montage expérimental est identique à celui du paragraphe relatif à l’extraction de l’enveloppe par méthode numérique faisant intervenir la transformation de Hilbert. Le développement permettant d’obtenir les amplitudes complexes des tensions $\underline V_1$ et $\underline V_2$ est identique à celui du premier paragraphe.
Le développement mathématique est identique au paragraphe relatif aux courbes de résonance à l’aide du détecteur de crête.[/peekaboo_content]
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : Courbes de résonance à l’aide de la detection de crête
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : Courbes de résonance à l’aide de la detection de crête
[download id="4170"]
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : courbe de résonance à l’aide de la transformée de Hilbert
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : courbe de résonance à l’aide de la transformée de Hilbert
[peekaboo_content][download id="4239"] [/peekaboo_content]
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : courbe de résonance à l’aide de la réponse impulsionnelle
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : courbe de résonance à l’aide de la réponse impulsionnelle
[peekaboo_content][download id="4269"][/peekaboo_content]
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : courbe de résonance à l’aide de la réponse indicielle
Expérience en vidéo
Couplage capacitif de deux circuits rLC identiques : courbe de résonance à l’aide de la réponse indicielle
