Effet photoélectrique-constante de Planck
- Mise en évidence expérimentale de l’effet photoélectrique,
- estimation de la constante de Planck.
Montage expérimental(schéma synoptique) 
Dispositif expérimental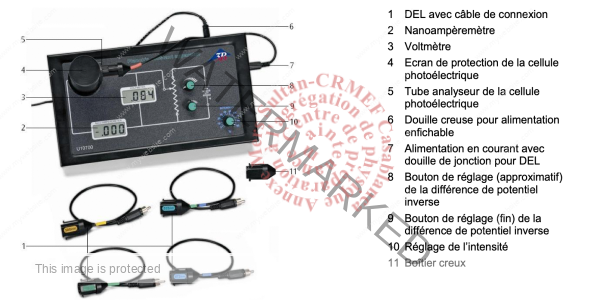
Dispositif constante de Planck
1. Définition de l’effet photoélectrique
C’est l’extraction des électrons d’un matériau excité par un rayonnement électromagnétique dont la fréquence dépasse un seuil. L’expérience montre que l’énergie des électrons extraits dépend de la fréquence du rayonnement et non de son intensité !
C’est Heinrich Hertz qui découvre accidentellement l’effet photoélectrique en 1887 alors qu’il s’intéressait à la production d’ondes électromagnétiques.2. Résultats expérimentaux obtenus historiquement
Le montage est donné dans la figure ci-dessous.
On éclaire une cathode métallique placée dans une cellule transparente sous vide. Dans des conditions particulières, on récupère les charges par l’anode A. Le courant et la tension dans la cellule sont contrôlés par l’ampèremètre et le voltmètre. On fait varier la tension UAC et on mesure le courant résultant.
On constate ce qui suit :
- Lorsqu’on éclaire la cathode par une radiation monochromatique, un courant peut circuler dans le circuit. Si la fréquence $\nu$ dépasse un seuil $\nu_0$ caractéristique du métal dont est constitué la cathode. La variation du courant avec la tension $U_{AC}$ est donné dans la figure ci-dessous.
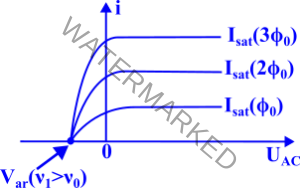
- Le photocourant de saturation est proportionnel au flux lumineux incident $\phi_0$,
- le curant est non nul pour des valeurs de $U_{AC}$ ngatives,
- lorsque $U_{AC}$ est égale à $V_{ar}$, appelé potentiel d’arrêt, le courant s’annule et ce quelque soit la valeur du flux $\phi_0$,
- le potentiel d’arrêt est une fonction linéaire de la fréquence comme le montre la figure ci-dessous.

2.1. Résultats explicables dans le cadre de la physique classique
- Résultat : lorsque on irradie une cathode métallique avec de la lumière ultraviolette : des électrons sont arrachés et sont accélérés par la différence de potentiel. Il en résulte un courant dans le circuit. Explication : Le champ électrique de l’onde exerce une force sur les électrons une force qui permet de les extraire si l’énergie est suffisante. La différence de potentiel accélère les électrons. Ces derniers atteignent l’anode et ainsi un courant s’établit dans le circuit.
- Résultat : à fréquence et puissance lumineuse donnée la variation de la tension anode-cathode $U_{AC}$ entraîne l’augmentation puis saturation du courant. Le courant de saturation est proportionnel à la puissance lumineuse ou flux $\phi_0$.
- Explication : la saturation correspond au cas où tous les électrons arrachés arrivent à l’anode. La proportionnalité entre le courant de saturation et la puissance lumineuse s’explique par le fait que le nombre d’électrons arrachés varie linéairement avec l’énergie absorbée.
- l’effet photoélectrique ne se manifeste que si la fréquence du rayonnement dépasse une fréquence seuil $\nu_0$
- l’existence d’une différence de potentiel négative appelée potentiel d’arrêt $V_{ar}$ au delà de laquelle le courant est nul. Celle-ci est indépendante de la puissance lumineuse. Elle varielinéairement avec la fréquence au dessus du seuil $\nu_0$. La pente de cette variation est la même pour tous les métaux : caractère universel.

Pour extraire un électron d’un métal, il faut que l’énergie du photon dépasse le travail de sortie caractéristique du métal(Work function) :$$\begin{array}{r}h \nu=W+E_{c} \\h \nu \geq W=h \nu_{0} \Rightarrow \nu \geq \nu_{0}\end{array}$$L’expression du potentiel d’arrêt s’obtient en utilisant la conservation de l’énergie mécanique du porteur de charge.$$\begin{array}{r}
E_{c}(C)+E_{p}(C)=E_{c}(A)+E_{p}(A) ; \quad E_{p}=q_{e} V \\q_{e}\left(V_{c}-V_{A}\right)=E_{c}(A)-h\left(\nu-\nu_{0}\right)\end{array}$$Le potentiel d’arrêt est la valeur de $U_{A C}=V_{A}-V_{C}$ lorsque $E_{C}(A)=0$. D’où son expression :$$V_{a r}=-\frac{h}{|q_{e}|}\left(\nu-\nu_{0}\right)$$Cette expression montre que le potentiel d’arrêt est indépendant du flux lumineux et la pente de $V_{a r}=f(\nu)$ est indépendante du métal(caractère universel de la pente).
Remarques :
Expérience en vidéo
Effet photoélectrique-constante de Planck
Expérience en vidéo
Effet photoélectrique-constante de Planck
