Simulation expérimentale du principe de fonctionnement d’un afficheur à cristal liquide noir-blanc.

Montage expérimental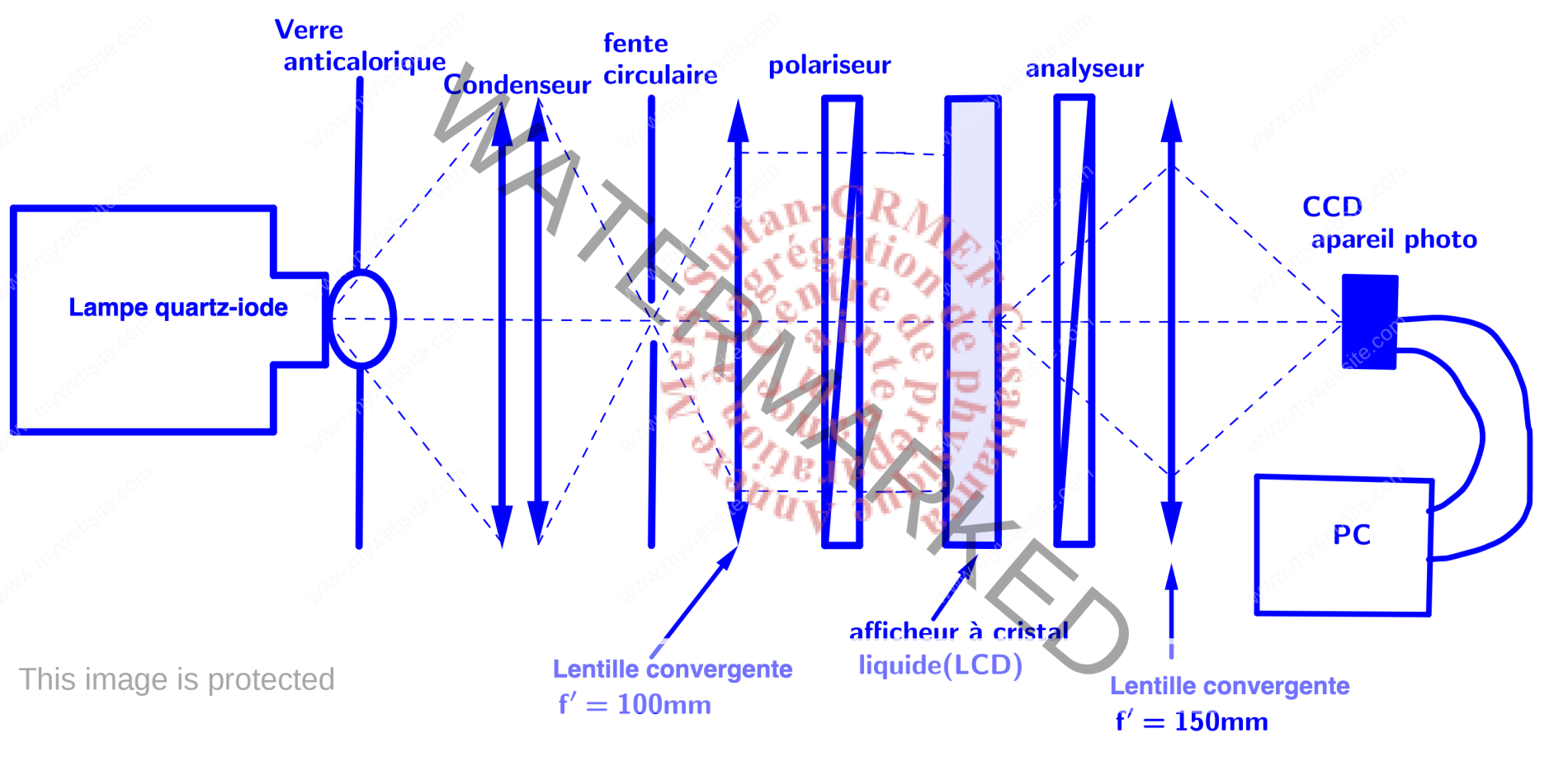

• lampe quartz-iode,
• filtre anticalorique,
• condenseur,
• fente circulaire
• lentille convergente : f’=100 mm ; f’=150, mm
• polariseurs,
• afficheur à cristal liquide didactique,
• écran,
• caméra à capteur CCD.

1. Définition

• Un cristal liquide est un matériau qui possède une structure intermédiaire entre le solide cristallin qui possède un ordre de position à grande distance et le liquide isotrope qui ne possède aucun ordre de position à grande distance,
• le cristal liquide est un fluide anisotrope à l’échelle moléculaire : il peut s’écouler et présente des propriétés telle que la biréfringence linéaire,
• deux familles sont à distinguer : les smectiques et les nématiques,
• la phase la plus utilisée dans les applications pratiques est la phase nématique,
• la phase nématique est formée de molécules allongées possédant une orientation moyenne qui confère à cette phase un ordre orientationnel à la différence du liquide isotrope,
• le domaine de température de la phase nématique d’un cristal liquide est le plus proche du liquide isotrope comme le montre la figure ci-dessous.

2. Le cristal liquide dans la nature La couleur irisée des élytres de ce coléoptère est due à l’organisation en cristal liquide des molécules de chitine.

© Peter Lanzersdorfer/Shutterstock.com

3. Spécificité d’un cristal liquide nématique

• Ancrage du nématique :  fixation de son orientation par la surface solide anisotrope sur laquelle est déposé,Transition de Frédericksz : au dessus d’un seuil de champ électrique appliqué, l’orientation du cristal liquide nématique devient parallèle à celle champ

• En absence de champ électrique appliqué, les molécules du cristal liquide changent leur orientation de manière progressive, de l’entrée à la sortie. À l’entrée les molécules se trouvent piégées dans les sillons à l’entrée. leur orientation est parallèle à la direction du polariseur $P_1$. À la sortie, leur orientation est contrôlée par les sillons à la sortie qui est parallèle à la direction du polariseur $P_2$. La lumière incidente est totalement transmise,
• En présence d’un champ appliqué dépassant le seuil de la transition de Fredericksz, les molécules sont orientées selon la direction du champ électrique parallèle à la direction de propagation. La lumière est éteinte par le deuxième polariseur perpendiculaire au premier.

4. Simulation expérimentale du principe de fonctionnement d’un afficheur à cristal liquide : intensité transmise L’expression de l’intensité transmise s’obtient moyennant le schéma ci-dessous.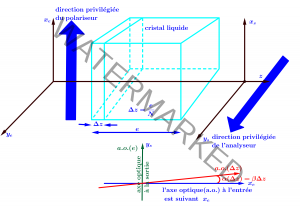

• On considère une lame de cristal liquide d’épaisseur e telle que à l’entrée les molécules sont orientées selon $Ox_e$(a.o parallèle à $Ox_e$) et à la sortie les molécules sont orientées selon $Oy_s$(a.o parallèle à $Oy_s$).
• On subdivise le cristal liquide en N tranches d’épaisseur $\Delta z = \frac{e}{N}$. Chaque tranche se comporte comme une lame homogène uniaxe. À la traversée d’une tranche le déphasage introduit est $\Delta n k_0\Delta z$ où $\Delta n=n_e-n_0$ est la biréfringence linéaire du cristal liquide, $n_o$ son indice ordinaire et $n_E$ son indice extraordinaire. $k_0=\frac{2\pi}{\lambda}$ est le nombre d’onde. L’axe optique tourne d’un angle $\alpha=\beta\Delta z$ tel que $\beta\ll\Delta nk_0$,
• l’axe optique tourne d’une tranche à l’autre jusqu’à la sortie où il devient parallèle à l’axe $(Oy_s)$

• Le vecteur excitation électrique subit les transformations selon le schéma ci-dessous,
• à la sortie du polariseur le vecteur excitation électrique s’exprime sous la forme : $$\overrightarrow D_p=\begin{pmatrix}D_{0x}\\ D_{0y}\end{pmatrix}_{/(Ox_{e},Oy_{e})}$$

• à la sortie de la première tranche, l’axe optique est porté par l’axe $(Ox_1)$ qui forme un angle $\beta\Delta z$ avec l’axe (0x). Le vecteur excitation électrique est  de la forme : \begin{eqnarray*}\overrightarrow D(\Delta z)=\exp(in_0k_0\Delta z)\begin{pmatrix}D_{0x}\exp(jk_0\Delta n\Delta z)\\D_{0y}\end{pmatrix}_{/(Ox_e,Oy_e)}\\\overrightarrow D(\Delta z)=\exp(in_0k_0\Delta z)A\begin{pmatrix}D_{0x}\\D_{0y}\end{pmatrix}_{/(Ox_1,Oy_1)} ;\\A=\begin{pmatrix}\cos(\beta\Delta z)\exp(jk_0\Delta n\Delta z)& \sin(\beta\Delta z)\\-\sin(\beta\Delta z)\exp(jk_0\Delta n\Delta z)&\cos(\beta\Delta z)\end{pmatrix}\\\beta\Delta z\ll \pi ; \ ;\Delta n\Delta zk_0\ll1\Rightarrow A=\begin{pmatrix}\exp(jk_0\Delta n\Delta z)& 0\\0& 1\end{pmatrix}\end{eqnarray*}
• à la sortie de la deuxième tranche, le vecteur excitation électrique devient sous la forme : $$\overrightarrow D(2\Delta z)=\exp(jn_0k_02\Delta z)A^2\begin{pmatrix}D_{0x}\\D_{0y}\end{pmatrix}_{(Ox_1,Oy_1)}$$

• à la sortie de la $N^{\text{ième}}$ tranche, $Ox_N$ est confondu avec $Oy_s$ et $Oy_N$ avec $Ox_s$. Le vecteur excitation électrique est de la forme : $$\overrightarrow D(N\Delta z)=\exp(jn_0k_0N\Delta z)A^N\begin{pmatrix}D_{Ox}\\D_{Oy}\end{pmatrix}_{/(Ox_N,Oy_N)=(Oy_s,Ox_s)}$$
• les composantes du vecteur excitation électrique à la sortie du cristal liquide dans la base $(Ox_s,Oy_s)$ s’expriment sous la forme : \begin{eqnarray*}\left\{\begin{gathered}D_{xs}=D_{0y}\exp(jn_0k_0e)\\D_{ys}=D_{0x}\exp(jn_0k_0e)\exp(j\Delta nk_0e)\end{gathered}\right.\end{eqnarray*}
• si le polariseur est orienté selon $Ox_e$ et l’analyseur est selon $(Oy_s)$, l’onde incidente est rectiligne selon $Ox_e$ ($D_{xs}=0$). L’onde émergente est polarisée rectilignement selon $Oy_s$. L’analyseur transmet intégralement cette polarisation. La polarisation n’a pas changé. Le dispositif se comporte comme un rotateur de polarisation.
• si le polariseur est orienté selon $Oy_e$ et l’analyseur est selon $(Oy_s)$, l’onde incidente est rectiligne selon $Oy_e$ ($D_{ys}=0$). À la sortie du cristal liquide l’onde est polarisée rectilignement selon $Ox_s$. L’onde n’est pas transmise par l’analyseur(extinction).

Lorsque le champ appliqué dépasse le seuil de la transition de Fredericksz, les molécules sont orientées selon la direction du champ électrique portée par $(Oz)$. Il en est de même pour l’axe optique c’est à dire qu’il ne subit plus de rotation continue entre la direction à l’entrée et celle à la sortie.

• En configuration polariseur perpendiculaire à l’analyseur, on obtient l’extinction. Ceci explique pourquoi les chiffres à 7 segments sont noires. Si on utilise un miroir pour observer l’onde réfléchie, les chiffres apparaissent sombres,
• lorsque le polariseur est parallèle à l’analyseur, les chiffres deviennent claires.

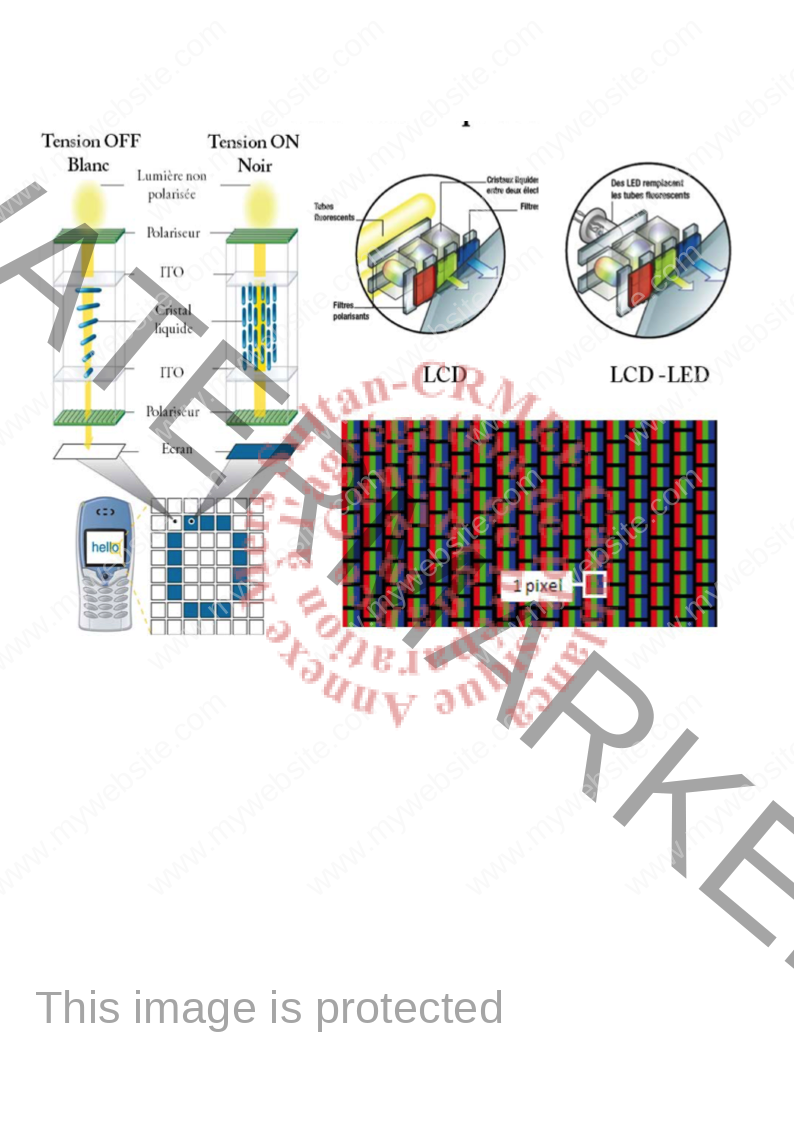
5. Afficheur à cristal liquide en couleur Le principe de fonctionnement est identique à celui de l’afficheur blanc-noire. Pour générer la couleur on utilise trois filtres pour chaque pixel comme le montre la figure c-dessous( référence : J.PIARD & al., « Synthèse d’un cristal liquide nématique : le MBBA », BUP,Vol. 109(2016)335-359).