Mise en évidence expérimentale de l’activité optique d’une solution de sucre(saccharose)
Étude de l’évolution de l’angle de rotation du plan de polarisation $\alpha$ en fonction de la longueur d’onde, de la concentration C et de la longueur L de la cuve.
Spectre cannelé dû au pouvoir rotatoire.
Montage expérimental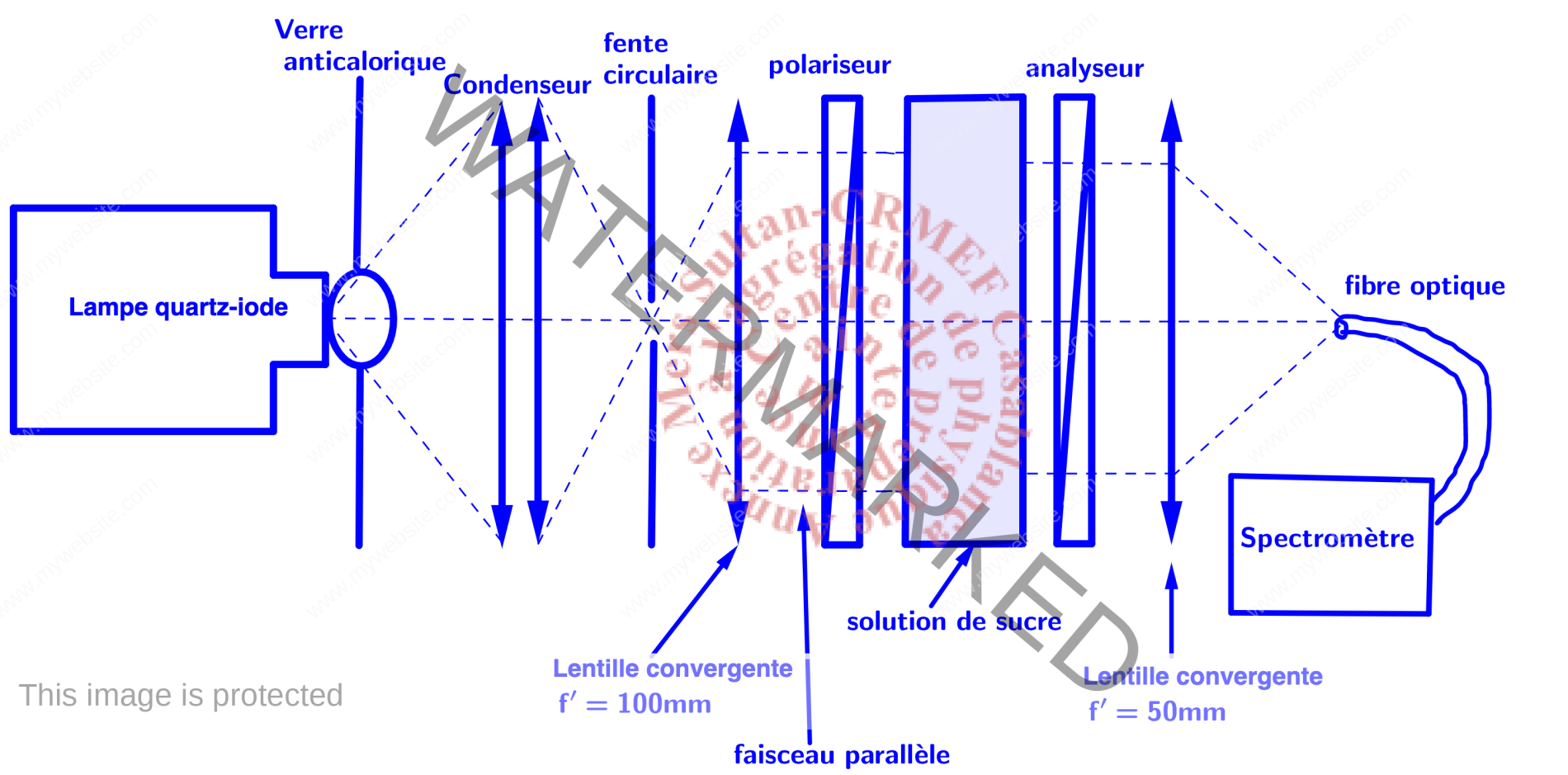
Montage expérimentale pour obtenir le spectre cannelé 
- lampe quartz-iode,
- filtre anticalorique,
- condenseur,
- fente circulaire
- lentille convergente : f’=100 mm ; f’=50, mm
- polariseurs,
- solution de sucre dans une cuve de différentes concentrations et de différentes longueurs
- écran,
- capteur à fibre optique,
- spectromètre.
1. Définition Un matériau présente le pouvoir rotatoire ou la la biréfringence circulaire si il fait tourner le plan de polarisation d’une lumière rectiligne incidente d’un angle $\alpha$ qui peut être positif ou négatif. On distingue deux types de matériaux :
- matériau dextrogyre : il fait tourner le plan de polarisation rectiligne incidente à droite pour un observateur situé en face du faisceau incident,
- matériau levogyre : il fait tourner le plan de polarisation rectiligne incidente à gauche pour un observateur situé en face du faisceau incident.
- Exemples : cristal de quartz, solution de saccharose, solution de glucose, solution de fructose,…
- Pour une longueur L et une concentration C on procède comme suit :
- initialement l’analyseur est croisé au polariseur. On tourne l’analyseur vers la droite jusqu’à ce qu’on obtienne le premier minimum.
- Ensuite, on détermine la longueur d’onde correspondante à ce minimum.
- On augmente l’angle 𝛂 de 5° par rapport à la dernière configuration vers la droite et on note la longueur d’onde du nouveau minimum,
- On refait le même travail jusqu’à ce qu’on obtienne un tableau de valeurs regroupant les longueurs d’onde et les angles correspondants.

Le problème c’est que la théorie cinématique de Fresnel ne permet de rendre compte parfaitement de la dépendance de l’angle de rotation du plan de polarisation en fonction de la longueur d’onde. 2.4. Interprétation de l’activité optique à l’aide de la théorie macroscopique électromagnétique La biréfringence circulaire trouve son origine dans le fait que la réponse est non locale : la polarisation électrique en un point M est due au champ électrique au point M et de la contribution du voisinage de M. Cette réponse peut être caractérisée par l’équation constitutive suivante : $$\overrightarrow P=\underbrace{\varepsilon_0\chi \overrightarrow E}_{\text{reponse locale}}+\underbrace{\varepsilon_0\gamma\overrightarrow{\operatorname{rot}}\overrightarrow E}_{\text{reponse non locale}}$$Le terme du rotationnel fait intervenir les dérivées partielles du champ électrique et rend compte de la contribution à la polarisation électrique du voisinage du point M. Le vecteur excitation électrique s’exprime sous la forme : $$\overrightarrow D=\varepsilon _0\varepsilon_r\overrightarrow E+\varepsilon_0\gamma\overrightarrow{\operatorname{rot}}\overrightarrow E$$ où $\varepsilon_r=1+\chi$ et $\gamma$ des constantes dépendant de la pulsation $\omega$.
On s’intéresse par la suite à la propagation des ondes planes progressives monochromatiques de la forme : $$\overrightarrow E=\overrightarrow E_0\exp[j(\omega t-\overrightarrow k\cdot\overrightarrow r)] ;\quad \overrightarrow k=n_0k_0\overrightarrow u_z$$ $n_0$ est l’indice ordinaire du quartz. On pose $\overrightarrow G=\gamma\overrightarrow k$ appelé vecteur gyration dont la norme est sans dimension. Le vecteur excitation électrique est relié au champ par un tenseur : $$\begin{pmatrix}D_{0x}\\D_{0y}\\D_{0z}\end{pmatrix}=\begin{pmatrix}n_0^2&-jG&0\\jG&n_0^2&0\\0&0&n_0^2\end{pmatrix}\begin{pmatrix}E_{0x}\\E_{0y}\\E_{0z}\end{pmatrix}$$Pour une onde plane circulaire gauche, on obtient l’indice de réfraction $n_g$ de la manière suivante : $$\overrightarrow E=\begin{pmatrix}E_0\\jE_0\\0\end{pmatrix}\Rightarrow \overrightarrow D=\varepsilon_0n_g^2\overrightarrow E ;\quad n_g^2=n_0^2+G$$On procède de même pour déterminer l’indice de réfraction relatif à une OPPM circulaire droite. Son expression est donnée sous la forme : $n_d^2=n_0^2-G$ Un développement au premier ordre conduit à l’expression de la biréfringence circulaire : $$\Delta n=n_d-n_g\approx \frac{-2\pi\gamma}{\lambda n_0}$$ L’angle de rotation du plan de polarisation est donné par : $$\alpha=\frac{\pi e\Delta n}{\lambda}=\frac{-2\pi^2\gamma}{\lambda^2n_0}$$ En tenant compte de la dépendance de $\gamma$ vis à vis de $\lambda$ et en poussant le développement de $\Delta n$ vers les ordres supérieurs on peut rendre compte de la dépendance de $\alpha$ avec la longueur d’onde selon l’équation de Sellmeier.
3. Spectre cannelé dû au pouvoir rotatoire du sucre 3.1. Quand est ce qu’on obtient un spectre cannelé ? Lorsqu’un montage optique éclairé par la lumière blanche introduit l’extinction de plusieurs longueurs d’onde du spectre visible. On peut l’obtenir :
- soit par interférence destructive dans le cas d’un système à division de front d’onde
- soit par interférence destructive dans le cas d’un système à division d’amplitude(dispositif deMichelson au voisinage du contact optique)
- soit par interférence destructive en lumière polarisée à l’aide d’une lame de quartz taillée parallèlement à son axe optique,
- soit par rotation du plan de polarisation jusqu’à cequ’il croise l’analyseur : c’est à dire à l’aide du pouvoir rotatoire. C’est cette méthode qu’on utilise dans ce qui suit.

Pour une direction de l’analyseur et une longueur d’onde données, l’intensité transmise par le montage s’exprime sous la forme : $$I(\lambda)=I_{0\lambda}\cos^2(\beta)=I_{0\lambda}\cos^2\left(\theta-\alpha\right) ;\quad \alpha=\frac{A}{\lambda^2-\lambda_0^2}$$L’intensité totale résultante suite à l’utilisation de la lumière blanche est la somme des intensités dues à chaque longueur d’onde : $$I_{\text{totale}}=\int \frac{dI_0}{d\lambda}\cos^2(\theta-\alpha(\lambda))d\lambda$$Pour une valeur de $\theta$, il existe certaines longueurs d’onde qui annulent l’intensité totale. Ce qui explique les cannelures obtenues.
Expérience en vidéo
Activité optique d’une solution de sucre
Expérience en vidéo
Activité optique d’une solution de sucre
[download id="7202"]
Expérience en vidéo
Spectre cannelé dû à l’activité optique d’une solution de sucre
Expérience en vidéo
Spectre cannelé dû à l’activité optique d’une solution de sucre
